Das handbuch der meeresinsel

Der chinesische Mathematiker Liu Hui verfasste im Jahre 263 einen Kommentar zu den Neun Büchern arithmetischer Technik. Nach seiner Überzeugung genügten die dort, insbesondere in Kapitel 9 vorgestellten geometrischen Methoden nicht, um geographische Vermessungen an faktisch unerreichbaren Messobjekten vorzunehmen.

Daraufhin fügte er dem neunten Kapitel der Neun Bücher arithmetischer Technik neun eigene Probleme hinzu, um genau diese Lücke in dieser Aufgabensammlung zu schließen.

Im siebenten Jahrhundert wurden Liu Huis neun Probleme aus den Neun Büchern arithme-tischer Technik wieder herausgenommen und als eigenständige Sammlung unter dem Titel Mathematisches Handbuch der Meeresinsel (Haidao Suan Ching) publiziert. Die Namensgebung beruht offenbar auf dem Inhalt der ersten Aufgabe.

Das Mathematische Handbuch der Meeresinsel enthält nun die folgenden neun Probleme:

1. Vermessung einer unerreichbaren Insel

2. Vermessung eines unerreichbaren Kiefernbaumes

3. Vermessung einer unerreichbaren Stadt I

4. Vermessung eines unerreichbaren Tals

5. Vermessung eines unerreichbaren Gebäudes

6. Vermessung einer unerreichbaren Flussmündung

7. Vermessung eines unerreichbaren Schwimmbeckens

8. Vermessung eines unerreichbaren Flusses

9. Vermessung einer unerreichbaren Stadt II

Eine englischsprachige Übersetzung und ausführliche Kommentierung dieser Aufgabensammlung, die wir für unsere Darstellung zur Grundlage nehmen, und aus der auch die obigen historischen Fakten stammen, findet sich in der Monographie

F.J. Swetz: The Sea Island Mathematical Manual (Pennsylvania State University Press, 1995).

Unsere Darstellung ist keine wörtliche Übersetzung dieses englischen Textes, sondern vielmehr dem Gebrauch an allgemeinen Schulen angepasst. Mit den Formulierungen lehnen wir uns außerdem K. Vogels deutscher Ausgabe der Neun Bücher arithmetischer Technik an.

Sämtliche Längeneinheiten des englischen Textes haben wir in Meter umgerechnet. Dabei liegen uns die folgenden Umrechnungen zugrunde (siehe K. Vogel, S. 139):

1 Li (Meile) entspricht 414 Meter
1 Chang (Klafter) entspricht 2,3 Meter
1 Bu (Schritt) entspricht 1,38 Meter
1 Ch'ih (Fuß) entspricht 0,23 Meter
1 Ts'un (Zoll) entspricht 0,023 Meter

Alle Abbildungen orientieren sich nach den entsprechenden Abbildungen aus der englischen Textausgabe, wurden aber mit dem Packet latex/pstricks neu erstellt.

Noch zu überarbeiten! Insbesondere Aufgaben 8 und 9!

Aufgabe 1: Vermessung einer unerreichbaren Insel pdf

Jetzt wollen wir eine Meeresinsel vermessen. Wir errichten zwei Pfähle gleicher Höhe, nämlich 6,9 Meter gemessen vom Boden. Der Abstand zwischen dem vorderen und dem hinteren Pfahl beträgt 1380 Meter. Wir nehmen an, dass die Insel, der vordere Pfahl und der hintere Pfahl in einer Linie ausgerichtet sind. Entferne dich nun 169,74 Meter vom vorderen Pfahl und beobachte den Gipfel der Insel von der Bodenoberfläche aus; es zeigt sich, dass dann die Spitze des vorderen Pfahls mit dem Gipfel übereinstimmt. Entferne dich nun 175,26 Meter vom hinteren Pfahl und beobachte wieder den Gipfel der Insel von der Bodenoberfläche aus; die Spitze des hinteren Pfahls stimmt dann ebenfalls mit dem Gipfel überein. Frage: Wie hoch ist die Insel, und wie weit ist sie vom vorderen Pfahl entfernt?

Gegebene Größen:

$AS$ und $CN$ sind die beiden Pfähle, gegeben sind $|AS|=|CN|=6,9$
$NS$ ist der Abstand der beiden Pfähle, gegeben ist $|NS|=1333$
der vordere Beobachtungspunkt ist in $B,$ gegeben ist $|BS|=169,74$
der hintere Beobachtungspunkt ist in $D,$ gegeben ist $|DN|=175,26$

Gesuchte Größen:

$PQ$ ist die Gipfelhöhe, gesucht ist
$QS$ ist die Entfernung zum vorderen Pfahl, gesucht ist

Außerdem fügen wir die zu $AB$ parallele Strecke $CT$ hinzu. $P$

Lösung: $|PQ|=1731,9$ Meter, $|QS|=42.435$ Meter

Aufgabe 2: Vermessung eines unerreichbaren Kiefernbaumes pdf

Jetzt wollen wir die Höhe eines Kiefernbaumes vermessen, der auf einem Hügel von ebenfalls unbekannter Höhe wächst. Wir errichten zwei Pfähle der gleichen Höhe 4,6 Meter auf dem Boden im gegenseitigen Abstand von 69 Meter. Wir nehmen an, dass der Baum, der vordere Pfahl und der hintere Pfahl in einer Linie ausgerichtet sind. Entferne dich nun 10,58 Meter vom vorderen Pfahl und beobachte den Gipfel des Kiefernbaumes von der Boden-oberfläche aus; es zeigt sich, dass dann die Spitze des vorderen Pfahles mit dem Gipfel des Baumes übereinstimmt. Betrachte aus dieser Position auch den Fuß des Baumes, der bez. des Pfahles 0,64 Meter unterhalb dessen Spitze zu liegen kommt. Entferne dich nun 12,19 Meter vom hinteren Pfahl und beobachte den Gipfel des Baumes von der Bodenoberfläche aus; es zeigt sich, dass dann die Spitze des Pfahles mit dem Gipfel des Baumes übereinstimmt. Frage: Wie hoch ist der Baum, und wie weit ist er vom vorderen Pfahl entfernt?

Gegebene Größen:

und sind die beiden Pfähle, gegeben sind
ist der Abstand der beiden Pfähle, gegeben ist
der vordere Beobachtungspunkt ist in gegeben ist
der hintere Beobachtungspunkt ist in gegeben ist
der Fuß des Baumes liegt auf dem Pfahl bei gegeben ist

Gesuchte Größen:

ist die Höhe des Kiefernbaumes, gesucht ist
ist die Entfernung zum vorderen Pfahl, gesucht ist

Lösung: $|AB|=28,07$ Meter, $|DK|=453,43$ Meter

Aufgabe 3: Vermessung einer unerreichbaren Stadt I

Jetzt wollen wir die Breite einer südlich gelegenen quadratischen Stadtmauer vermessen. Errichte zwei Pfähle, 13,8 Meter voneinander in Ostrichtung entfernt, die beide auf Augenhöhe stehen und durch eine Schnur verbunden sind. Der östliche Pfahl befinde sich mit der südöstlichen und der nordöstlichen Ecke der Stadtmauer auf einer Linie. Entferne dich nun 6,9 Meter nordwärts vom östlichen Pfahl und betrachte die nordwestliche Ecke der Stadtmauer; die Sichtlinie schneidet die Schnur, die die Pfähle verbindet, 5,2095 Meter von seinem östlichen Ende aus gesehen. Entferne dich nun 18,4 Meter nordwärts vom östlichen Pfahl und betrachte die nordwestliche Ecke der Stadtmauer; es zeigt sich, dass dann diese Ecke und der westliche Pfahl auf der Beobachtungslinie liegen. Frage: Was ist die Seitenlänge der quadratischen Stadtmauer, und wie weit ist die Stadt vom östlichen Pfahl entfernt?

Gegebene Größen:

die Stadt wird durch $ODGH$ begrenzt
die beiden Pfähle befinden sich in $C$ und gegeben ist $|CF|=13,8$
der erste Beobachtungspunkt ist in $B,$ gegeben ist $|BC|=6,9$
die erste Sichtlinie schneidet die Schnur in $E,$ gegeben ist $|CE|=5,2095$
der zweite Beobachtungspunkt ist in $A,$ gegeben ist $|AC|=18,4$

Gesuchte Größen:

$GH$ ist die Seitenlänge der Stadtmauer, gesucht ist $|GH|$
$CD$ ist die Entfernung zur Stadtmauer, gesucht ist $|CD|$

Lösung: $|CD|=1718,1$ Meter, $|DG|=1302,375$ Meter

Aufgabe 4: Vermessung eines unerreichbaren Tals

Jetzt wollen wir die Tiefe eines Tals vermessen. Errichte dazu einen nach oben geöffneten Zimmermannswinkel der Höhe 1,38 Meter am Rand des Tals. Betrachte die entgegengesetzte Seite der Talsohle von der Spitze des Zimmermannswinkels aus; es zeigt sich, dass dann die Talsohle in einer Linie liegt mit der Spitze des Winkels und der Markierung 2,093 Meter auf der Erweiterung seiner Basis. Errichte nun einen weiteren, ähnlichen, nach oben geöffneten Zimmermannswinkel über dem ersten; der Abstand zwischen den Basen beider Winkel ist 6,9 Meter. Betrachte wieder die entgegengesetzte Seite der Talsohle von der Spitze des oberen Winkels aus; es zeigt sich, dass dann die Talsohle in einer Linie liegt mit der Spitze des oberen Winkels und der Markierung 1,955 Meter auf der Erweiterung der Basis dieses Winkels. Frage: Wie tief ist das Tal?

Gegebene Größen:

die Tal ist $ABCP$
die Beobachtungspunkte sind $E$ und $H$
die Höhen der Zimmermannswinkel sind $CE$ und $FH$ , gegeben ist $|CE|=|FH|=1,38$
die verlängerten Basen der Winkel sind $CD$ und $FG$ , gegeben sind $|CD|=2,093$ und
der Abstand der Basen der Winkel ist $CF$ , gegeben ist $|CF|=6,9$ $|FG|=1,955$

Gesuchte Größen:

$BC$ ist die Tiefe des Tals, gesucht ist $|BC|$

Lösung: $|BC|=96, 37$ Meter

Aufgabe 5: Vermessung eines unerreichbaren Gebäudes

Jetzt wollen wir die Höhe eines Gebäudes vermessen. Wir stehen dazu auf einem Berggipfel, das Gebäude befindet sich auf einer Höhe mit dem Fuß des Berges. Errichte einen nach oben geöffneten Zimmermannswinkel der Höhe 1,38 Meter auf dem Berggipfel. Betrachte, nach unten schauend, den Fuß des Gebäudes von der oberen Spitze des Winkels aus; es zeigt sich, dass dann der Fuß des Gebäudes in einer Linie liegt mit der oberen Spitze des Winkels und der Markierung 2,76 Meter auf der Verlängerung seiner Basis. Errichte nun einen weiteren, ähnlichen, nach oben geöffneten Zimmermannswinkel über dem ersten auf; der Abstand der Basen beider Winkel ist 6,9 Meter. Betrachte, nach unten schauend, den Fuß des Gebäudes von der oberen Spitze des oberen Winkels aus; es zeigt sich, dass dann der Fuß des Gebäudes in einer Linie liegt mit der oberen Spitze des oberen Winkels und der Markierung 2,622 Meter auf der Verlängerung der Basis dieses Winkels. Errichte schließlich an dieser zweiten Markierung einen kleinen Pfahl auf der Höhe der Basis des oberen Zimmermannswinkels und betrachte, nach unten schauend, von der oberen Spitze des oberen Winkels aus den Dachgiebel des Gebäudes; es zeigt sich, dass dann dieser Giebel in einer Linie liegt mit der oberen Spitze des oberen Winkels und der nach oben verlaufenden Markierung 0,184 Meter auf dem kleinen Pfahl. Frage: Wie hoch ist das Gebäude?

Gegebene Größen:

das Gebäude wird nach oben durch $A$ und $B$ begrenzt
die Beobachtungspunkte sind $C$ und $E$
die Höhen der Zimmermannswinkel sind $CD$ und $EF$ , gegeben ist $|CD|=|EF|=1,38$
die verlängerten Basen der Winkel sind $DO$ und $FH$ , gegeben sind $|DO|=2,622$ und $|FH|=2,76$
der Abstand der Basen der Winkel ist $DF$ , gegeben ist $|DF|=6,9$
der kleine Pfahl wird in $O$ errichtet, gegeben ist $|JO|=0,184$

Gesuchte Größen:

es ist $AB$ die Höhe des Gebäudes, gesucht ist $|AB|$

Lösung: $18,4$ Meter

Aufgabe 6: Vermessung einer unerreichbaren Flussmündung

Jetzt wollen wir die Breite einer südöstlich gelegenen Flussmündung vermessen. Errichte dazu zwei Pfähle in nordsüdlicher Ausrichtung; der Abstand zwischen diesen Pfählen ist 20,7 Meter, und sie werden durch eine auf dem Boden verlaufende Schnur miteinander verbunden. Blicke nach Westen und entferne dich 13,8 Meter westwärts vom nördlichen Pfahl. Beobachte von dort aus das südliche Flussufer der Flussmündung auf Niveau der Bodenoberfläche; es zeigt sich, dass dieses südliche Ufer in einer Linie liegt mit dem Beobachtungspunkt und der Markierung 9,246 Meter auf der Schnur, gemessen von deren nördlichem Ende. Betrachte nun von demselben Beobachtungspunkt das nördliche Flussufer; es zeigt sich, dass dieses nörliche Ufer in einer Linie liegt mit dem Beobachtungspunkt und der Markierung 6,486 Meter auf der Schnur, wieder gemessen von deren nördlichem Ende. Entferne dich nun 31,05 Meter westwärts vom nördlichen Pfahl und beobachte das südliche Ufer der Flussmündung; es zeigt sich, dass dieses südliche Ufer in einer Linie mit dem neuen Beobachtungspunkt und dem südlichen Pfahl liegt. Frage: Wie breit ist die Flussmündung?

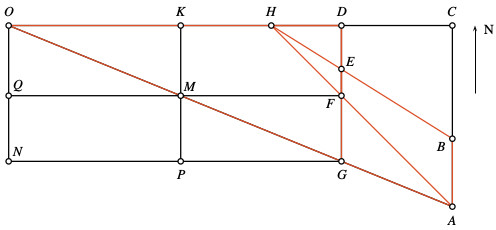
Gegebene Größen:

es ist $AB$ die Flussmündung
die Pfähle sind in $D$ und $G$
der Abstand der beiden Pfähle ist $DG$ , gegeben ist $|DG|=20,7$
die erste Beobachtungspunkt ist in $H$ , gegeben ist $|DH|=13,8$
die Pfähle sind durch die Schnur $DG$ miteinander verbunden
gegeben sind $|DE|=2,76$ und $|DF|=9,246$
der zweite Beobachtungspunkt ist in $O$ , gegeben ist $|DO|=31,05$

Gesuchte Größen:

$AB$ ist die Breite der Flussmündung, gesucht ist $|AB|$

Lösung: $|AB|=690$ Meter

Die englische Textquelle enthält die Strecke $|EF|=2,76$ als gegebene Größe. Da die Aufgabenstellung aber eventuell missverstanden werden kann, haben wir stattdessen in die Aufgabe die Strecke $DE$ eingearbeitet.

Aufgabe 7: Vermessung eines unerreichbaren Wasserlochs

Jetzt wollen wir die Tiefe eines Wasserlochs vermessen, welches klares Wasser mit weißen Steinen auf dem Grund enthält. Errichte dazu einen Zimmermannswinkel der Höhe 0,69 Meter an der oberen Kante des Lochs; es zeigt sich, dass dann die Wasseroberfläche auf der entgegengesetzten Seite des Lochs in einer Linie liegt mit der oberen Spitze des Winkels und der Markierung 1,035 Meter auf der Verlängerung seiner Basis, während der Grund des Wasserlochs auf dieser Seite und auf diese Weise mit 0,552 Metern gemessen wird. Errichte jetzt einen weiteren, ähnlichen Zimmermannswinkel über dem ersten Winkel; der Abstand der Basen beider Winkel ist 0,92 Meter. Schaue von der oberen Spitze dieses oberen Winkels abwärts; es zeigt sich, dass dann die Wasseroberfläche auf der entgegengesetzten Seite des Lochs in einer Linie liegt mit der oberen Spitze des oberen Winkels und der Markierung 0,92 Meter auf der Verlängerung seiner Basis, während der Grund des Wasserlochs auf dieser Seite und auf diese Weise mit 0,506 Metern gemessen wird. Frage: Wie tief ist das Wasser?

Gegeben Größen:

das Wasserbecken ist $ABHG$
die Höhe beider Zimmermannswinkels ist $EF$, gegeben ist $|EF|$=0,69
der Abstand der Basen beider Winkel ist $FQ$, gegeben ist $|FQ|=0,92$
der erste Beobachtungspunkt ist in $E$, gegeben sind $|FK|=1,035$ und $|FL|=0,552$
der zweite Beobachtungspunkt ist in $P$, gegeben sind $|QR|=0,92$ und $|QS|=0,506$

Gesuchte Größen:

$AB$ ist die Tiefe des Wasserbeckens, gesucht ist $|AB|$

Lösung: $|AB|=2,76$ Meter

Aufgabe 8: Vermessung eines unerreichbaren Flusses

Jetzt wollen wir die Breite eines südlich eines Berges gelegenen Flusses vermessen. Errichte dazu einen Zimmermannswinkel der Höhe 2,76 Meter auf dem Gipfel des Berges. Schaue abwärts von der oberen Spitze des Winkels auf das südliche Ufer des Flusses; es zeigt sich, dass dieses südliche Ufer in einer Linie liegt mit der oberen Spitze des Winkels und der Markierung 3,013 Meter auf der Verlängerung seiner Basis. Betrachte aus dieser Beobachtungsposition auch das nördliche Ufer des Flusses; es zeigt sich, dass dieses nördliche Ufer in einer Linie liegt mit der oberen Spitze des Winkels und der Markierung 0,529 Meter auf seiner Basis. Erklimme nun eine weitere Anhöhe, nämlich 70,38 Meter höher und 30,36 Meter nach Norden. Errichte erneut den Zimmermannswinkel und betrachte das südliche Ufer; es zeigt sich, dass dieses südliche Ufer in einer Linie liegt mit der oberen Spitze des Winkels und der Markierung 2,76 Meter auf seiner Basis. Frage: Wie breit ist der Fluss?

Gegeben Größen:

die Breite des Flusses ist durch $AB$ gegeben
die Höhe der Zimmermannswinkel ist $LK$ = $PG$ , gegeben ist $LK$ =2,76
gegeben ist $|HK|=70,38$ und $|GH|=30,36$
der erste Beobachtungspunkt ist in $P$ , gegeben sind $|EG|=3,013$ und $|EF|$ =2,484
der zweite Beobachtungspunkt ist in $L$ , gegeben ist $|JK|=2,76$

Gesuchte Größen:

$AB$ ist die Breite des Flusses, gesucht ist $|AB|$

Lösung: $|AB|=976,02$ Meter

Die englische Textquelle enthält die Strecke als gegebene Größe. Da die Aufgabenstellung aber eventuell missverstanden werden kann, haben wir stattdessen in die Aufgabe die Reststrecke $FG$ eingearbeitet.

Aufgabe 9: Vermessung einer unerreichbaren Stadt II

Wir wollen nun die Breite und die Länge einer südlich eines Berges befindlichen Stadt vermessen. Errichte dazu einen Zimmermannswinkel der Höhe 0,805 Meter und gleich langer Basis auf dem Gipfel des Berges. Die obere Spitze des Winkels liege auf einer Linie mit der südöstlichen Ecke und der nordöstlichen Ecke der Stadt. Betrachte die nordöstliche Ecke der Stadt von der oberen Spitze des Winkels aus; es zeigt sich, dass diese nordöstliche Ecke in einer Linie liegt mit der oberen Spitze des Winkels und einem Punkt auf der Verlängerung seiner Basis, nämlich 2,76 Meter vom äußeren Basisende entfernt. Drehe nun den aufrechten Arm des Winkels horizontal und lege den Winkel an den ursprünglichen Beobachtungspunkt. Betrachte die nordwestliche Ecke der Stadt von der neuen oberen Spitze des Winkels aus; es zeigt sich, dass diese nordwestliche Ecke in einer Linie liegt mit der neuen oberen Spitze des Winkels und einem Punkt auf der Verlängerung seiner neuen Basis, nämlich 1,15 Metern vom äußeren Basisende entfernt. Betrachte jetzt die südöstliche Ecke der Stadt von der oberen Spitze des Winkels in seiner ursprünglichen Lage aus; es zeigt sich, dass diese südöstliche Ecke in einer Linie liegt mit der ursprünglichen oberen Spitze des Winkels und einem Punkt auf der Verlängerung seiner ursprünglichen Basis, nämlich 4,14 Metern vom äußeren Basisende entfernt. Errichte jetzt einen weiteren, ähnlichen Zimmermannswinkel über dem ersten Winkel; der Abstand der Basen beider Winkel ist 9,2 Meter. Betrachte die südöstliche Ecke der Stadt von der oberen Spitze des oberen Winkels aus; es zeigt sich, dass diese südöstliche Ecke in einer Linie liegt mit der oberen Spitze des oberen Winkels und einem Punkt auf der Verlängerung seiner Basis, nämlich 4,025 Metern vom äußeren Basisende entfernt. Frage: Was sind die Breite und die Länge der Stadt?