Hausaufgabenblatt 4
Aufgabe HA 13
Es sei \( \mathbb K \) ein angeordneter Körper. Beweisen Sie:
| (i) | Dreiecksungleichung |
\[ |x+y|\le|x|+|y|\quad\mbox{für alle}\ x,y\in\mathbb K \]
| (ii) | inverse Dreiecksungleichung |
\[ \big||x|-|y|\big|\le|x-y|\quad\mbox{für alle}\ x,y\in\mathbb K. \]
Lösung
| (i) | Seien \( x,y\ge 0. \) Dann sind |
| und die geforderte Ungleichung folgt aus |
| Seien \( x,y\lt 0. \) Dann sind \( x+y\lt 0 \) sowie |
| und die geforderte Ungleichung folgt aus |
| Seien \( x\ge 0, \) \( y\lt 0 \) und \( x+y\ge 0. \) Dann sind |
| und die geforderte Ungleichung folgt aus |
| Seien \( x\ge 0, \) \( y\lt 0 \) und \( x+y\lt 0. \) Dann sind |
| und die geforderte Ungleichung folgt aus |
| Den Fall \( x\lt 0, \) \( y\ge 0 \) behandelt man analog. | |
| (ii) | Mit der Dreiecksungleichung erhalten wir |
| Ganz entsprechend ermitteln wir |
| Wir fassen zusammen |
Damit ist alles gezeigt.\( \qquad\Box \)
Aufgabe HA 14
Beweisen Sie, dass folgende Zahlen nicht rational sind.
| (i) | \( \sqrt{2}+\sqrt{6} \) |
| (ii) | \( \sqrt{2}+\sqrt{3} \) |
Lösung
| (i) | Angenommen, \( \sqrt{2}+\sqrt{6} \) ist rational. Dann ist auch rational |
\[ \big(\sqrt{2}+\sqrt{6}\big)^2=2+2\,\sqrt{2}\,\sqrt{6}+6=8+2\,\sqrt{2}\,\sqrt{6}\,, \]
| und damit sind auch rational \( 2\,\sqrt{2}\,\sqrt{6} \) sowie \( \sqrt{2}\,\sqrt{6}, \) und wegen \( \sqrt{6}=\sqrt{2}\,\sqrt{3} \) sind auch rational \( \sqrt{2}\,\sqrt{2}\,\sqrt{3}=2\,\sqrt{3} \) bzw. \( \sqrt{3}. \) Das ist ein Widerspruch zur Präsenzaufgabe 15. Es ist also \( \sqrt{2}+\sqrt{6} \) nicht rational. | |
| (ii) | Angenommen, \( \sqrt{2}+\sqrt{3} \) ist rational. Dann ist auch rational |
\[ (\sqrt{2}+\sqrt{3})^2=2+2\,\sqrt{2}\,\sqrt{3}+3=5+2\,\sqrt{2}\,\sqrt{3}\,, \]
| und damit sind auch rational \( 2\,\sqrt{2}\,\sqrt{3} \) bzw. \( \sqrt{2}\,\sqrt{3} \) bzw. \( \sqrt{6}. \) Das ist ein Widerspruch zur Präsenzaufgabe 16. Es ist also \( \sqrt{2}+\sqrt{3} \) nicht rational. |
Damit ist alles gezeigt.\( \qquad\Box \)
Aufgabe HA 15
Wie in Präsenzaufgabe 17, jetzt aber für die folgende Skizze
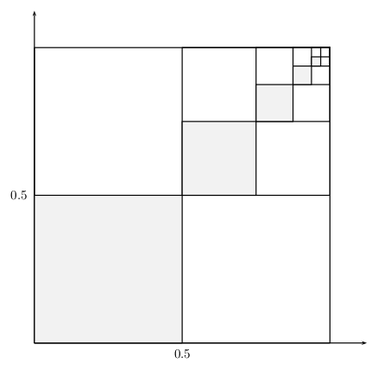
Lösung
Ignorieren wir das Feld rechts oben, so verbleiben \( 2 \) große weiße Felder und \( 1 \) großes graues Feld. Im nächsten Schritt sehen wir wieder \( 2 \) weiße Felder und ein entsprechend großes graues Feld, allerdings viermal kleiner als das erste graue Feld. Das geht immer so weiter, d.h. es ist \[ \lim_{n\to\infty}\sum_{k=1}^n\frac{1}{4^k}=\frac{1}{3}\,. \]
Aufgabe HA 16
Betrachten Sie den folgenden rekursiven Konstruktionsprozess:
| 1. | Beginne mit einer geraden Strecke der Länge \( 1 \) (Menge \( C_0 \)). |
| 2. | Lösche das mittlere Drittel von \( C_0 \) (ohne die beiden Randpunkte links und rechts dieses mittleren Drittels; Ergebnis ist die Menge \( C_1 \)). |
| 3. | Lösche die mittleren Drittel von \( C_1 \) (ohne die linken und rechten Randpunkte des Geöschten; Ergebnis ist die Menge \( C_2 \)) usw. |
Die Cantorsche Mittel-Drittel-Menge \( C\subset\mathbb R \) ist dann definiert als der Durchschnitt \[ C:=\bigcap_{k=0}^\infty C_k\,. \] Welche Länge besitzen \( C_0, \) \( C_1, \) \( C_2 \) usw. sowie \( C \) selbst?
Lösung
Wir benutzen die Schreibweise \[ [a,b]:=\{x\in\mathbb R\,:\,a\le x\le b\}\,. \] Es hat nun \( C_0=[0,1] \) die Länge \[ \ell(C_0)=1=\left(\frac{2}{3}\right)^0\,. \] Weiter hat \( C_1=\left[0,\frac{1}{3}\right]\cup\left[\frac{2}{3},1\right] \) die Länge \[ \ell(C_1)=\frac{1}{3}+\frac{1}{3}=\frac{2}{3}=\left(\frac{2}{3}\right)^1, \] und \( C_2=\left[0,\frac{1}{9}\right]\cup\left[\frac{2}{9},\frac{3}{9}\right]\cup\left[\frac{6}{9},\frac{7}{9}\right]\cup\left[\frac{8}{9},1\right] \) besitzt die Länge \[ \ell(C_2)=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{4}{9}=\left(\frac{2}{3}\right)^2 \] usw. Allgemein gilt \[ \ell(C_n)=\left(\frac{2}{3}\right)^n\longrightarrow 0\quad\mbox{für}\ n\to\infty\,. \] Die Cantorsche Mittel-Drittel-Menge besitzt also die Länge \( 0.\qquad\Box \)
