Catenoid-Helicoid isometry
The parametrization
\[ \begin{array}{l} x(u,v):=(\cosh u\cos v\cos\alpha+\sinh u\sin v\sin\alpha), \\ y(u,v):=(\cosh u\sin v\cos\alpha-\sinh u\cos v\sin\alpha), \\ z(u,v):=(u\cos\alpha+v\sin\alpha) \end{array} \]
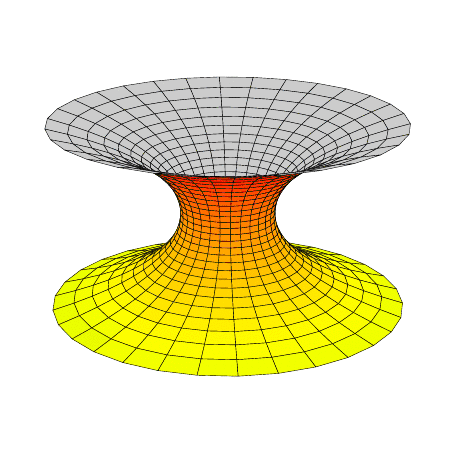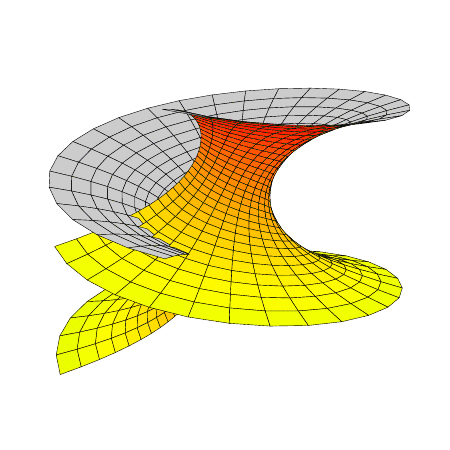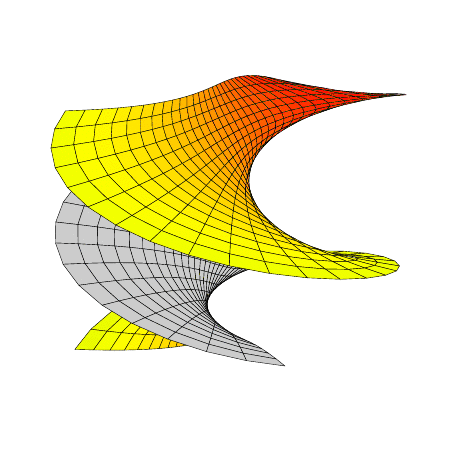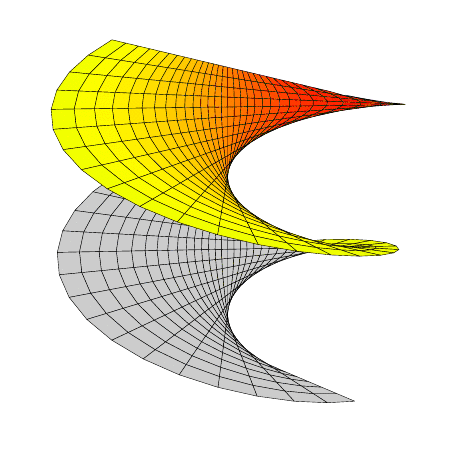
represents a one-parameter family of conformally parametrized minimal surfaces; \( \alpha=0 \) gives the catenoid, \( \alpha=\frac{\pi}{2} \) the helicoid
generated with ps-tricks
Peckham, S.D.: Solutions to nonlinear partial differential equations: a geometric approach (1999)
Catenoid–Helicoid Isometry
Isometry
$$ X_\alpha(u,v)= \begin{pmatrix} c\!\left(\cos (u)\,\cosh (\!\frac{v}{c})\,\cos (\alpha) + \sin (u)\,\sinh (\!\frac{v}{c})\,\sin (\alpha )\right) \\ c\!\left(\sin (u)\,\cosh(\!\frac{v}{c})\,\cos\alpha - \cos (u) \,\sinh(\!\frac{v}{c})\,\sin(\alpha)\right) \\ v\,\cos(\alpha) + c\,u\,\sin(\alpha) \end{pmatrix},\quad u\in[0,2\pi),\; v\in\mathbb{R}. $$Special cases
$$ X_{0}(u,v)=\bigl(c\,\cosh(\tfrac{v}{c})\cos (u),\;c\,\cosh(\tfrac{v}{c})\sin (u),\;v\bigr)\quad(\text{Catenoid}). $$ $$ X_{\pi/2}(u,v)=\bigl(c\,\sinh(\tfrac{v}{c})\sin ( u),\;-c\,\sinh(\tfrac{v}{c})\cos (u),\;c\,u\bigr)\quad(\text{Helicoid}). $$- Left mouse button: rotate
- Right mouse button: pan
- Mouse wheel: zoom
Created by Yannick Häberlin with WebGL (part of his Bachelor thesis)