| 14. Das Lebesguesche Maß | 15. Lebesguemessbare Funktionen | 16. Das Lebesguesche Integral |
| 17. Sätze über Lebesgueintegrierbare Funktionen | 18. Das Hausdorffsche Maß | 20. Integralsätze |
19. Potentialtheorie
Wir beginnen mit der
Definition: Eine Abbildung \( f\colon\Omega\to\mathbb R^n \) auf einer offenen Menge \( \Omega\subseteq\mathbb R^n \) bezeichnen wir als ein Vektorfeld.
Zwei Beispiele solcher Vektorfelder sind
| \( \circ \) | das Gravitationsfeld als Zentralfeld mit einer Quelle als Zentrum |
| \( \circ \) | das Magnetfeld als quellenfreies Rotationsfeld |
Wir empfehlen die Wikipedia-Seiten zum ➝ Gravitationsfeld und zum ➝ magnetischen Feld.
Definition: Es sei \( \Omega\subseteq\mathbb R^n \) eine offene Menge. Dann erklären wir die Divergenz der Abbildung \[ f(x)=(f_1(x_1,\ldots,x_n),\ldots,f_n(x_1,\ldots,x_n))\in C^1(\Omega,\mathbb R^n) \] an der Stelle \( x\in\Omega \) gemäß \[ \mbox{div}\,f(x):=\sum_{i=1}^n\frac{\partial f_i(x)}{\partial x_i}\,. \]
Die Divergenz lässt sich auch als Spur der Jacobimatrix \( \partial f(x) \) schreiben, genauer \[ \mbox{div}\,f(x) =\mbox{Spur}\,\partial f(x) =\mbox{Spur} \left( \begin{array}{ccc} f_{1,x_1} & \cdots & f_{1,x_n} \\ \vdots & & \vdots \\ f_{n,x_1} & \cdots & f_{n,x_n} \end{array} \right) =\sum_{i=1}^n\frac{\partial f_i(x)}{\partial x_i}\,. \]
Häufig verwendet man folgende Sprechweisen:
| \( \circ \) | Es heißt der Punkt \( x_0\in\Omega \) eine Quelle, falls gilt \( \mbox{div}\,f(x_0)\gt 0. \) |
| \( \circ \) | Es heißt der Punkt \( x_0\in\Omega \) eine Senke, falls gilt \( \mbox{div}\,f(x_0)\lt 0. \) |
Wir erinnern schließlich an den Nablaoperator bzw. Gradienten einer Funktion \( f\colon\Omega\subseteq\mathbb R^n\to\mathbb R \) \[ \nabla f(x)\equiv\mbox{grad}\,f(x):=\left(\frac{\partial f(x)}{\partial x_1}\,,\ldots,\frac{\partial f(x)}{\partial x_n}\right). \]
Achten Sie im Folgenden auf die Dimension \( n=3. \)
Definition: Es sei \( \Omega\subseteq\mathbb R^3 \) eine offene Menge. Dann erklären wir die Rotation der Abbildung \[ f(x)=(f_1(x_1,x_2,x_3),f_2(x_1,x_2,x_3),f_3(x_1,x_2,x_3))\in C^1(\Omega,\mathbb R^3) \] an der Stelle \( x\in\Omega \) gemäß \[ \mbox{rot}\,f(x) :=\left( \frac{\partial f_3(x)}{\partial x_2}-\frac{\partial f_2(x)}{\partial x_3}\,, \frac{\partial f_1(x)}{\partial x_3}-\frac{\partial f_3(x)}{\partial x_1}\,, \frac{\partial f_2(x)}{\partial x_1}-\frac{\partial f_1(x)}{\partial x_2}\,, \right). \]
Auch hier vereinbaren wir:
| \( \circ \) | Ein Vektorfeld heißt wirbelfrei, falls dessen Rotation identisch verschwindet. Andernfalls heißt es ein Wirbelfeld. |
Mit dem Nablaoperator bzw. Gradienten schreibt man auch hier gelegentlich symbolisch \[ \mbox{rot}\,f(x)=\nabla\times f(x). \]
19.1.4 Potentiale und Gradientenfelder
Im Zentrum des vorliegenden Kapitels stehen Potentiale und Gradientenfelder. Dazu zunächst die
Definition: Auf der offenen Menge \( \Omega\subseteq\mathbb R^n \) sei die Abbildung \( f\colon\Omega\to\mathbb R^n \) gegeben. Eine differenzierbare Abbildung \( \varphi\colon\Omega\to\mathbb R \) mit der Eigenschaft \[ \mbox{grad}\,\varphi(x)=f(x)\quad\mbox{in}\ \Omega \] heißt ein Potential von \( f(x). \) Umgekehrt heißt \( f(x) \) ein Gradientenfeld, wenn ein Potential \( \varphi(x) \) von \( f(x) \) existiert.
Der folgende, als Übung zu beweisende Satz beinhaltet eine notwendige Bedingung an ein Vektorfeld, ein Gradientenfeld zu sein. Achten Sie aber hierbei auf die Dimensionszahl \( n=3. \)
Satz: Es seien \( \Omega\subseteq\mathbb R^3 \) offen und \( \varphi\in C^2(\Omega,\mathbb R) \) ein Potential des Gradientenfeldes \( f\colon\Omega\to\mathbb R^3. \) Dann gilt \[ \mbox{rot}\,f(x)=0\quad\mbox{in}\ \Omega. \] Mit anderen Worten:
| \( \to \) | Gradientenfelder sind wirbelfrei. |
Notwendige und hinreichende Bedingungen allgemeiner Vektorfelder, Gradientenfelder zu sein, werden wir im nächsten Abschnitt kennenleren.
19.1.5 Laplaceoperator und harmonische Funktionen
Definition: Es sei \( \Omega\subseteq\mathbb R^n \) eine offene Menge. Dann erklären wir den Laplaceoperator der Abbildung \[ f(x)=f(x_1,\ldots,x_n)\in C^2(\Omega,\mathbb R) \] an der Stelle \( x\in\Omega \) gemäß \[ \Delta f(x):=\mbox{div}\,\mbox{grad}\,f(x). \]
Der Laplaceoperator spielt in der Theorie der partiellen Differentialgleichungen zweiter Ordnung die grundlegende Rolle.
Die einfachste partielle Differentialgleichung zweiter Ordnung ist die sogenannte Laplacegleichung \[ \Delta f(x)=0\quad\mbox{in}\ \Omega. \] Sie muss noch vervollständigt werden durch Randbedingungen o.ä., zum Beispiel durch Vorgabe von \( f(x) \) auf dem Rand \( \partial\Omega. \)
Eine Funktion, die der Laplacegleichung genügt, heißt harmonisch.
19.1.6 Aufgaben und Wiederholungsfragen
| 1. | Was versteht man unter einem Vektorfeld? | ||||||||
| 2. | Skizzieren Sie die folgenden ebenen Vektorfelder, und erläutern Sie kurz: | ||||||||
|
|||||||||
| Hier dazu ein ➝ Geogebra-Applet. | |||||||||
| 3. | Berechnen Sie die Divergenz der folgenden Vektorfelder \( f_i\in C^1(\mathbb R^3,\mathbb R^3), \) und werten Sie die Divergenz jeweils im angegebenen Punkt \( (x_0,y_0,z_0)\in\mathbb R^3 \) aus. | ||||||||
|
|||||||||
| 4. | Wie ist der Gradient einer Funktion \( f\in C^1(\mathbb R^n,\mathbb R) \) definiert? | ||||||||
| 5. | Berechnen Sie den Gradienten der folgenden Funktionen \( f_i\in C^1(\mathbb R^3,\mathbb R), \) und werten Sie den Gradienten jeweils im angegebenen Punkt \( (x_0,y_0,z_0)\in\mathbb R^3 \) aus. | ||||||||
|
|||||||||
| 6. | Wie ist die Rotation eines Vektorfeldes \( f\in C^1(\mathbb R^3,\mathbb R^3) \) definiert? | ||||||||
| 7. | Berechnen Sie die Rotation der folgenden Vektorfelder \( f_i\in C^1(\mathbb R^3,\mathbb R^3), \) und werten Sie die Rotation jeweils im angegebenen Punkt \( (x_0,y_0,z_0)\in\mathbb R^3 \) aus. | ||||||||
|
|||||||||
| 8. | Wann heißt eine differenzierbare Abbildung \( \varphi\colon\mathbb R^n\to\mathbb R \) ein Potential? | ||||||||
| 9. | Wann heißt eine Abbildung \( f\colon\mathbb R^n\to\mathbb R^n \) ein Gradientenfeld? | ||||||||
| 10. | Es seien \( \Omega\subseteq\mathbb R^3 \) und \( \varphi\in C^2(\Omega,\mathbb R) \) ein Potential des Gradientenfeldes \( f\colon\Omega\to\mathbb R^3. \) Beweisen Sie, dass dann gilt |
\[ \mbox{rot}\,f(x)=0\quad\mbox{in}\ \Omega. \]
| 11. | Es seien \( f,g\colon\mathbb R^3\to\mathbb R \) stetig differenzierbare Funktionen, \( a,b\colon\mathbb R^3\to\mathbb R^3 \) stetig differenzierbare Vektorfelder und \( \lambda,\mu\in\mathbb R. \) Beweisen Sie: | ||||||
|
|||||||
| 12. | Wie ist der Laplaceoperator einer Funktion \( f\in C^2(\mathbb R^n,\mathbb R) \) definiert? | ||||||
| 13. | Wann heißt eine Funktion \( f\in C^2(\mathbb R^n,\mathbb R) \) harmonisch? | ||||||
| 14. | Beweisen Sie, dass die folgenden Funktionen \( f_i\in C^2(\mathbb R^3,\mathbb R) \) harmonisch in \( \mathbb R^3 \) sind. | ||||||
|
|||||||
| 15. | Wie müssen \( a,b,c\in\mathbb R \) gewählt sein, damit die Funktion |
\[ f(x,y)=ax^2+2bxy+cy^2\,,\quad(x,y)\in\mathbb R^2\,, \]
| harmonisch in \( \mathbb R^2 \) ist? | |
| 16. | Es seien \( f,g\in C^2(\mathbb R^n,\mathbb R). \) Beweisen Sie |
\[ \Delta(fg)=f\Delta g+2\langle\nabla f,\nabla g\rangle+g\Delta f \]
| mit dem Euklidischen Skalarprodukt \( \langle\cdot,\cdot\rangle. \) |
Rechenaufgaben: 2, 3, 5, 7, 10, 11, 14, 15, 16
19.2.1 Zusammenhang und Wegzusammenhang
Definition: Eine nichtleere Menge \( \Omega\subseteq\mathbb R^n \) heißt
| \( \circ \) | zusammenhängend, wenn für alle offenen Mengen \( U,V\subseteq\mathbb R^n \) mit \( \Omega\subseteq U\cup V \) und \( U\cap V=\emptyset \) richtig ist |
\[ U\cap\Omega=\emptyset\quad\mbox{oder}\quad V\cap\Omega=\emptyset; \]
| \( \circ \) | wegzusammenhängend, wenn zu je zwei Punkten \( x,y\in\Omega \) eine vollständig in \( \Omega \) verlaufende, stetige, die Punkte \( x \) und \( y \) verbindende Kurve existiert, d.h. eine stetige Abbildung |
\[ \gamma\colon[0,1]\longrightarrow\Omega \quad\mbox{mit}\quad \gamma(0)=x,\ \gamma(1)=y. \]
Satz: Es sei \( \Omega\subseteq\mathbb R^n \) offen und nichtleer. Dann sind äquivalent:
| (i) | \( \Omega \) ist zusammenhängend. |
| (ii) | \( \Omega \) ist wegzusammenhängend. |
| (iii) | Für alle \( x,y\in\Omega \) existiert eine vollständig in \( \Omega \) verlaufende, stückweise stetig differenzierbare Kurve \( \gamma\colon[0,1]\to\Omega \) mit \( \gamma(0)=x \) und \( \gamma(1)=y. \) |
| (iv) | Für alle \( x,y\in\Omega \) existiert ein vollständig in \( \Omega \) verlaufender, stetiger Polygonzug \( \pi(x,y), \) der die Punkte \( x \) und \( y \) verbindet. |
In diesem Satz bedeuten
| \( \circ \) | \( \gamma\colon[0,1]\to\Omega \) eine stückweise stetig differenzierbare Kurve, wenn die Abbildung \( \gamma(t) \) stetig auf \( [0,1] \) ist und eine endliche Zerlegung von \( [0,1] \) existiert, |
\[ 0=t_0\lt t_1\lt t_2\lt\ldots\lt t_N=1,\quad N\in\mathbb N, \]
| so dass \( \gamma(t) \) auf jedem \( [t_{i-1},t_i], \) \( i=1,\ldots,N, \) stetig differenzierbar ist. | |
| \( \circ \) | die Vereinigungsmenge |
\[ \pi(x,y):=\overline{x_1x_2}\cup\overline{x_2x_3}\cup\ldots\cup\overline{x_{N-1}x_N}\subset\mathbb R^n \] ein stetiger Polygonzug, worin \( \overline{x_ix_{i+1}}:=\{x_i+t(x_{i+1}-x_i)\,:\,t\in[0,1]\} \) die Verbindungsstrecke zwischen zwei Knotenpunkten \( x_i,x_{i+1}\in\mathbb R^n \) des Polygonzugs bezeichnet.
Beachten Sie in diesem Satz ferner, dass \( \Omega\subseteq\mathbb R^n \) eine offene Menge ist. In allgemeinen topologischen Räumen, wie wir sie in der Analysis 2 kennengelernt haben, ist dieser Satz nicht richtig. Wir verweisen auf folgende, inhaltlich jeweils unterschiedlich ausgerichtete Literatur, die Sie auch online in unserer Bibliothek erhalten:
Beweis des Satzes
Wir gehen in mehreren Schritten vor.
| 1. | Wir zeigen die Implikation Aussage (i)\( \to \)(iv). |
| Es sei \( \Omega\subseteq\mathbb R^n \) zusammenhängend. Seien weiter \( x,y\in\Omega \) zwei Punkte, die sich nicht durch einen Polygonzug verbinden lassen. Betrachte nun die Mengen |
\[ \begin{array}{l} U:=\{z\in\Omega\,:\,\mbox{es existiert ein stetiger Polygonzug}\ \pi(x,z)\subset\Omega\}\,, \\ V:=\{z\in\Omega\,:\,\mbox{es existiert kein stetiger Polygonzug}\ \pi(x,z)\subset\Omega\}\,. \end{array} \]
| Zunächst sind \( U \) und \( V \) offen, denn (hier nur für \( U, \) die Offenheit von \( V \) zeigt man analog): | |||
|
|||
| Ferner überlegt man sich |
\[ \Omega=U\cup V \quad\mbox{sowie}\quad U\cap V=\emptyset\,, \]
| und die Mengen \( U \) und \( V \) sind nicht leer wegen \( x\in U \) und \( y\in V. \) Damit haben wir aber einen Widerspruch zum Zusammenhang von \( \Omega, \) d.h. zwei beliebige Punkte \( x,y\in\Omega \) lassen sich doch durch einen stetigen Polygonzug miteinander verbinden. | |
| 2. | Wir zeigen die Implikation Aussage (iv)\( \to \)(iii). |
| Jeder stetige Polygonzug kann gleichzeitig als stückweise stetig differenzierbare Kurve angesehen werden. | |
| 3. | Wir zeigen die Implikation Aussage (iii)\( \to \)(ii). |
| Die Aussage folgt direkt aus der Definition des Wegzusammenhangs. | |
| 4. | Wir zeigen die Implikation Aussage (ii)\( \to \)(i). |
| Es sei \( \Omega\subseteq\mathbb R^n \) wegzusammenhängend. Seien ferner \( U,V\subseteq\mathbb R^n \) zwei nichtleere, offene Mengen mit |
\[ \Omega\subseteq U\cup V \quad\mbox{und}\quad U\cap V=\emptyset\,. \]
| Angenommen, es gelten |
\[ U\cap\Omega\not=\emptyset \quad\mbox{und}\quad V\cap\Omega\not=\emptyset\,, \]
| und es existieren \( x,y\in\Omega \) mit \( x\in U\cap\Omega \) und \( y\in V\cap\Omega. \) Nach Voraussetzung gibt es eine stetige Abbildung |
\[ \gamma\colon[0,1]\longrightarrow\Omega \quad\mbox{mit}\quad \gamma(0)=x,\ \gamma(1)=y, \]
| d.h. es gelten \( \gamma(0)\in U \) und \( \gamma(1)\not\in U. \) Wir definieren |
\[ t^*:=\sup\{t\in[0,1]\,:\,\gamma([0,t])\subset U\}\,. \]
| Nun entnehmen wir auf Grund der Stetigkeit der Abbildung \( \gamma(t) \) sowie der Offenheit der Mengen \( U \) und \( V \) | |||||
|
|||||
| Für ein derartiges \( t\in(\widetilde t,t^*) \) ist also \( \gamma(t)\in U\cap V \) im Widerspruch zur Annahme \( U\cap V=\emptyset. \) Es muss also \( U\cap\Omega=\emptyset \) oder \( V\cap\Omega=\emptyset \) gelten, d.h. \( \Omega \) ist zusammenhängend. |
Damit ist alles bewiesen.\( \qquad\Box \)
Definition: Unter einem Gebiet verstehen wir eine nichtleere, offene und zusammenhängende Menge \( \Omega\subseteq\mathbb R^n. \)
Definition: Ein Gebiet \( \Omega\subseteq\mathbb R^n \) heißt sternförmig, falls ein \( x\in\Omega \) existiert, so dass gilt \[ \overline{xy}\subset\Omega\quad\mbox{für alle}\ y\in\Omega. \]
Beispielsweise sind konvexe Gebiete sternförmig, und jedes sternförmige Gebiet ist zusammenhängend.
Der spezielle Punkt \( x\in\Omega \) in der Definition heißt Zentrumspunkt. Sternförmige Gebiete können mehrere Zentrumspunkte besitzen.
19.2.3 Existenz von Gradientenfeldern
Wir widmen uns nun der Frage nach der Existenz von Gradientenfeldern. Zunächst dazu folgendes notwendige Kriterium, dessen Beweis wir als Übung belassen.
Satz: Auf der offenen Menge \( \Omega\subseteq\mathbb R^n \) sei das stetig differenzierbare Gradientenfeld \( f\colon\Omega\to\mathbb R^n \) mit dem zweimal stetig partiell differenzierbarem Potential \( \varphi\colon\Omega\to\mathbb R \) gegeben. Dann gelten die Integrabilitätsbedingungen \[ \frac{\partial f_i(x)}{\partial x_j}=\frac{\partial f_j(x)}{\partial x_i}\quad\mbox{in}\ \Omega \] für alle \( i,j=1,\ldots,n. \)
Auf sternförmigen Gebieten sind die Integrabilitätsbedingungen sogar hinreichend, wie unser zweites Kriterium lehrt.
Satz: Es sei \( \Omega\subseteq\mathbb R^n \) ein sternförmiges Gebiet mit Zentrumspunkt \( x_0\in\Omega. \) Sei ferner \( f\colon\Omega\to\mathbb R^n \) eine stetig differenzierbare Abbildung mit \[ \frac{\partial f_i(x)}{\partial x_j}=\frac{\partial f_j(x)}{\partial x_i}\quad\mbox{in}\ \Omega \] für alle \( i,j=1,\ldots,n. \) Dann ist \( f(x) \) ein Gradientenfeld und besitzt das Potential \[ \varphi(x):=\int\limits_0^1\langle f(x_0+t(x-x_0)),x-x_0\rangle\,dt. \]
Beweis
Zunächst macht man sich klar, dass \[ \varphi(x) =\int\limits_0^1\langle f(x_0+t(x-x_0)),x-x_0\rangle\,dt =\int\limits_0^1\sum_{i=1}^nf_i(x_0+t\delta)\delta_i\,dt \] mit \( \delta:=x-x_0, \) \( \delta=(\delta_1,\ldots,\delta_n)\in\mathbb R^n, \) stetig partiell differenzierbar ist. Für den Integranden berechnen wir die erste partielle Ableitung \[ \begin{array}{lll} \displaystyle \frac{\partial}{\partial x_j}\,\sum_{i=1}^nf_i(x_0+t\delta)\delta_i\negthickspace & = & \negthickspace\displaystyle \sum_{i=1}^n\frac{\partial}{\partial x_j}\,f(x_0+t\delta)\delta_i \\ & = & \negthickspace\displaystyle \sum_{i=1}^n\frac{\partial f_i(x_0+t\delta)}{\partial x_j}\,t\delta_i+f_j(x_0+t\delta). \end{array} \] Zusammen mit den Integrabilitätsbedingungen \( \partial_{x_j}f_i=\partial_{x_i}f_j \) folgt daher \[ \begin{array}{lll} \displaystyle \frac{\partial\varphi(x)}{\partial x_j}\negthickspace & = & \negthickspace\displaystyle \int\limits_0^1\left\{\sum_{i=1}^n\frac{\partial f_i(x_0+t\delta)}{\partial x_j}\,t\delta_i+f_j(x_0+t\delta)\right\}dt \\ & = & \negthickspace\displaystyle \int\limits_0^1\left\{\sum_{i=1}^n\frac{\partial f_j(x_0+t\delta)}{\partial x_i}\,t\delta_i+f_j(x_0+t\delta)\right\}dt \\ & = & \negthickspace\displaystyle \int\limits_0^1\frac{d}{dt}\,\Big[tf_j(x_0+t\delta)\Big]\,dt \,=\,f_j(x_0+\delta) \,=\,f_j(x) \end{array} \] für alle \( j=1,\ldots,n \) und für alle \( x\in\Omega. \) Insgesamt folgt also \[ \nabla\varphi(x)=f(x)\quad\mbox{in}\ \Omega. \] Das beweist den Satz.\( \qquad\Box \)
19.2.4 Aufgaben und Wiederholungsfragen
| 1. | Wann heißt eine nichtleere Menge \( \Omega\subseteq\mathbb R^n \) zusammenhängend? | ||||
| 2. | Wann heißt eine nichtleere Menge \( \Omega\subseteq\mathbb R^n \) wegzusammenhängend? | ||||
| 3. | Welchen Zusammenhang zwischen Zusammenhang und Wegzusammenhang für offene Mengen im \( \mathbb R^n \) kennen Sie? | ||||
| 4. | Skizzieren Sie jeweils wenigstens ein Beispiel für eine zusammenhängende und für eine nicht zusammenhängende Menge im | ||||
|
|
|||||
| 5. | Was versteht man unter einem sternförmigen Gebiet? | ||||
| 6. | Skizzieren Sie jeweils zwei Beispiele für ein sternförmiges und für ein nicht sternförmiges Gebiet. Markieren Sie insbesondere die Zentrumspunkte. | ||||
| 7. | Beweisen Sie den ersten Satz aus Paragraph 19.2.3. | ||||
| 8. | Begründen Sie durch Verifizieren der Integrierbarkeitsbedingungen, ob in den folgenden Fällen Gradientenfelder vorliegen, und bestimmen Sie ggf. ein Potential. | ||||
|
|||||
| 9. | Begründen Sie durch Verifizieren der Integrierbarkeitsbedingungen, ob in den folgenden Fällen Gradientenfelder vorliegen, und bestimmen Sie ggf. ein Potential. | ||||
|
|||||
| 10. | Wir betrachten die Abbildung |
\[ f(x,y) :=\left\{ \begin{array}{cl} \displaystyle \left(\frac{(x^4-y^4)y+4x^2y^3}{(x^2+y^2)^2}\,,\frac{(x^4-y^4)x-4x^3y^2}{(x^2+y^2)^2}\right), & (x,y)\not=(0,0) \\ 0, & (x,y)=(0,0) \end{array} \right.. \]
|
\[ \varphi(x,y) :=\left\{ \begin{array}{cl} \displaystyle \frac{(x^2-y^2)xy}{x^2+y^2}\,, & \mbox{falls}\ (x,y)\not=(0,0) \\ 0, & \mbox{falls}\ (x,y)=(0,0) \end{array} \right. \]
|
\[ \frac{\partial f_1(x,y)}{\partial x_2}=\frac{\partial f_2(x,y)}{\partial x_1}\quad\mbox{in}\ \mathbb R^2\,. \]
| Benutzen Sie dazu ohne weitere Begründung die Ergebnisse aus dem in der Vorlesung Analysis 2, ➝ Paragraph 13.3.3 vorgestelltem Beispiel. |
Rechenaufgaben: 4, 6, 7, 8, 9, 10
19.3.1 Kurven und ihre Parametrisierungen
Wir wollen nun Integrale über Kurven \( C\subset\mathbb R^n \) in Euklidischen Räumen studieren.
Zunächst müssen wir aber den Begriff der „Kurve“ präzisieren und knüpfen dazu an unsere Untersuchungen aus der Vorlesung ➝ Analysis 2, Abschnitt 12.1 an. Wir betrachten also zwei stetig partiell differenzierbare Kurvenparametrisierungen \[ \gamma\colon[a,b]\longrightarrow\mathbb R^n \quad\mbox{und}\quad \widetilde\gamma\colon[\widetilde a,\widetilde b]\longrightarrow\mathbb R^n\,. \]
Reguläre Kurven
Für solche Kurvenparametrisierungen sei Folgendes richtig:
| \( \circ \) | Es existiert eine reguläre Parametertransformation, d.h. eine \( C^1 \)-reguläre, diffeomorphe Abbildung |
\[ \varphi\colon[\widetilde a,\widetilde b]\longrightarrow[a,b] \]
| mit einer stetig differenzierbaren Inversen \( \varphi^{-1}\colon[a,b]\to[\widetilde a,\widetilde b] \) und der Eigenschaft |
\[ \dot\varphi(\widetilde t)\not=0\quad\mbox{für alle}\ \widetilde t\in[\widetilde a,\widetilde b],\quad\mbox{wobei}\quad \dot\varphi(\widetilde t):=\frac{d}{d\widetilde t}\,\varphi(\widetilde t) \]
| (orientierungstreu, falls \( \dot\varphi(\widetilde t)\gt 0, \) sonst orientierungsumkehrend), so dass gilt |
\[ \gamma(\varphi(\widetilde t))=\widetilde\gamma(\widetilde t),\quad\widetilde t\in[\widetilde a,\widetilde b]. \]
| \( \circ \) | Die Kurvenparametrisierung \( \gamma\in C^1([a,b],\mathbb R^n) \) genüge ferner der folgenden geometrischen Regularitätsbedingung |
\[ |\dot\gamma(t)|\gt 0\quad\mbox{für alle}\ t\in[a,b]. \] Eine solche analytisch wie geometrisch reguläre Kurvenparametrisierung \( \gamma(t) \) bezeichnen wir kurz als regulär - siehe aber die Bemerkung unten.
Die Abbildung \( \gamma(t) \) und ihre reguläre Umparametrisierung \( \widetilde\gamma(\widetilde t) \) heißen äquivalent, in Zeichen \[ \gamma\sim\widetilde\gamma. \] Bei \( \sim \) handelt es sich tatsächlich um eine Äquivalenzrelation: Mit \( \gamma(t) \) ist auch \( \widetilde\gamma(\widetilde t) \) regulär.
Oft wird nun die Äquivalenzklasse \( [\gamma] \) aller zur regulären Kurvenparametrisierung \( \gamma(t) \) äquivalenten Kurvenparametrisierungen als reguläre Kurve definiert. Wir können uns dieser Definition stillschweigend anschließen, wollen aber vor allem mit dem Bild \[ C=\mbox{Spur}\,\gamma(t)\subset\mathbb R^n \] der Parametrisierung rechnen und bezeichnen daher auch die Menge \( C\subset\mathbb R^n \) als reguläre Kurve. Eine genaue Definition wollen wir aber auslassen.
Bemerkung: Neben diesen regulären Kurvenparametrisierungen ist es wichtig, auch Parametrisierungen zuzulassen, die stetig, aber nur stückweise stetig differenzierbar sind, d.h. es gibt eine Zerlegung \[ a=t_0\lt t_1\lt t_2\lt\ldots\lt t_N=b,\quad N\in\mathbb N, \] so dass \( \gamma(t) \) auf jedem \( [t_{i-1},t_i], \) \( i=1,\ldots,N, \) stetig differenzierbar ist, siehe Paragraph 19.2.1 oben. Wir werden darauf jeweils aufmerksam machen.
19.3.2 Definition des Kurvenintegrals
Definition: Es seien \( \Omega\subseteq\mathbb R^n \) offen und \( C\subset\Omega \) eine reguläre Kurve mit Parametrisierung \( \gamma\colon[a,b]\to\Omega. \) Unter dem Kurvenintegral einer Abbildung \( f\in C^0(\Omega,\mathbb R^n) \) entlang \( C\subset\Omega \) verstehen wir \[ \begin{array}{lll} \displaystyle \int\limits_C\langle f(x),dx\rangle\negthickspace & \equiv & \negthickspace\displaystyle \int\limits_\gamma\langle f(x),dx\rangle \,\equiv\,\int\limits_\gamma\big\{f_1(x)\,dx_1+\ldots+f_n(x)\,dx_n\big\} \\ & := & \negthickspace\displaystyle \int\limits_a^b\langle f(\gamma(t)),\dot\gamma(t)\rangle\,dt \,=\,\sum_{i=1}^n\int\limits_a^bf_i(\gamma(t))\dot\gamma_i(t)\,dt. \end{array} \]
Ohne Beweis halten wir fest
Satz Seien \( \Omega\subseteq\mathbb R^n \) offen, \( C\subset\Omega \) eine reguläre Kurve mit Parametrisierung \( \gamma(t) \) und \( \widetilde\gamma=\gamma\circ\varphi(\widetilde t) \) eine positiv orientierte, reguläre Umparametrisierung, d.h. worin gilt \[ \dot\varphi(\widetilde t)\gt 0\quad\mbox{für alle}\ \widetilde t\in[\widetilde a,\widetilde b]. \] Dann gilt \[ \int\limits_{\widetilde\gamma}\langle f(x),dx\rangle=\int\limits_\gamma\langle f(x),dx\rangle\,. \]
Kurvenintegrale sind also geometrische Größen und hängen nicht von ihrer parametrischen Beschreibung ab, solange wir nur positiv orientierte Umparametrisierungen zulassen, was nachträglich die nichtparametrische Schreibweise \[ \int\limits_C\langle f(x),dx\rangle \] rechtfertigt.
Bemerkung: Sind die Kurve \( C\subset\mathbb R^n \) und damit die Parametrisierung \( \gamma\colon[a,b]\to\mathbb R^n \) stetig, aber nur stückweise stetig differenzierbar, wie in der Bemerkung in Paragraph 19.3.1 beschrieben, so setzen wir für das Kurvenintegral \[ \int\limits_C\langle f(x),dx\rangle :=\sum_{i=0}^{N-1}\int\limits_{t_i}^{t_{i+1}}\langle f(x),dx\rangle\,. \]
19.3.3 Zusammengesetzte Kurven
Es seien \[ \gamma\colon[a,b]\longrightarrow\mathbb R^n\,,\quad \gamma_1\colon[c,d]\longrightarrow\mathbb R^n\,,\quad \gamma_2\colon[d,e]\longrightarrow\mathbb R^n \] reguläre, aber nur stückweise stetig differenzierbare Kurvenparametrisierungen mit \( \gamma_1(d)=\gamma_2(d). \) Dann definieren wir
| \( \circ \) | die Summe von \( \gamma_1 \) und \( \gamma_2 \) als |
\[ \omega:=\gamma_1+\gamma_2\colon[c,e]\longrightarrow\mathbb R^n \quad\mbox{vermöge}\quad \omega(t) :=\left\{ \begin{array}{cl} \gamma_1(t), & \mbox{falls}\ t\in[c,d] \\ \gamma_2(t), & \mbox{falls}\ t\in[d,e] \end{array} \right. \]
| \( \circ \) | die Inverse von \( \gamma \) als |
\[ \gamma^{-1}\colon[a,b]\longrightarrow\mathbb R^n \quad\mbox{vermöge}\quad \gamma^{-1}(t):=\gamma(a+b-t),\ t\in[a,b]. \] Die Abbildungen \( \gamma(t) \) und \( \gamma^{-1}(t) \) besitzen dieselben Spuren im \( \mathbb R^n, \) allerdings mit entgegengesetztem Durchlaufsinn.
Einen Beweis des folgenden Satzes belassen wir als Übung.
Satz: Auf der offenen Menge \( \Omega\subseteq\mathbb R^n \) seien \( f,g\in C^0(\Omega,\mathbb R^n). \) Seien ferner \( \alpha,\beta\in\mathbb R \) und \[ \gamma\colon[a,b]\longrightarrow\Omega\,,\quad \gamma_1\colon[c,d]\longrightarrow\Omega\,,\quad \gamma_2\colon[d,e]\longrightarrow\Omega \] reguläre, stückweise stetig differenzierbare Kurvenparametrisierungen mit \( \gamma_1(d)=\gamma_2(d). \) Dann gelten
| (i) | \( \displaystyle\int\limits_\gamma\langle\alpha f(x)+\beta g(x),dx\rangle=\alpha\int\limits_\gamma\langle f(x),dx\rangle+\beta\int\limits_\gamma\langle g(x),dx\rangle \) |
| (ii) | \( \displaystyle\int\limits_{\gamma^{-1}}\langle f(x),dx\rangle=-\int\limits_\gamma\langle f(x),dx\rangle \) |
| (iii) | \( \displaystyle\int\limits_{\gamma_1+\gamma_2}\langle f(x),dx\rangle=\int\limits_{\gamma_1}\langle f(x),dx\rangle+\int\limits_{\gamma_2}\langle f(x),dx\rangle \) |
Die Kurvenintegrale sind dabei wie in der Bemerkung in Paragraph 19.3.2 zu verstehen.
19.3.4 Kurvenintegrale über Gradientenfelder
Für Gradientenfelder lassen sich Kurvenintegrale besonders leicht berechnen.
Satz: Es seien \( \Omega\subseteq\mathbb R^n \) offen und \( C\subset\Omega \) eine reguläre Kurve mit regulärer Parametrisierung \( \gamma\colon[a,b]\to\Omega. \) Ferner sei \( f\colon\Omega\to\mathbb R^n \) eine Abbildung mit dem Potential \( \varphi\in C^1(\Omega,\mathbb R). \) Dann gilt \[ \int\limits_C\langle f(x),dx\rangle=\varphi(\gamma(b))-\varphi(\gamma(a)). \]
Beweis
Wir berechnen nämlich \[ \begin{array}{lll} \displaystyle \int\limits_C\langle f(x),dx\rangle\negthickspace & = & \negthickspace\displaystyle \int\limits_a^b\langle f(\gamma(t)),\dot\gamma(t)\rangle\,dt \,=\,\int\limits_a^b\sum_{i=1}^nf_i(\gamma(t))\dot\gamma_i(t)\,dt \\ & = & \negthickspace\displaystyle \int\limits_a^b\sum_{i=1}^n\frac{\partial\varphi(\gamma(t))}{\partial x_i}\,\dot\gamma_i(t)\,dt \,=\,\int\limits_a^b\frac{d}{dt}\,\varphi(\gamma(t))\,dt \\ & = & \negthickspace\displaystyle \varphi(\gamma(b))-\varphi(\gamma(a)). \end{array} \] Das war zu zeigen.\( \qquad\Box \)
Dieses Resultat besagt, dass für Gradientenfelder das Kurvenintegral nur vom Anfangs- und Endpunkt der Kurve abhängt, nicht jedoch von ihrem sonstigen Verlauf selbst. Entlang einfach geschlossener Kurven verschwindet daher in dieser Situation das Kurvenintegral.
Bemerkung: Der Satz kann genauso auch für stetige, aber nur stückweise stetig differenzierbare Kurven formuliert werden.
19.3.5 Wegunabhängigkeit von Kurvenintegralen
Definition: Es sei \( \Omega\subseteq\mathbb R^n \) ein Gebiet. Eine Abbildung \( f\in C^0(\Omega,\mathbb R^n) \) heißt wegunabhängig in \( \Omega, \) falls für alle \( x,y\in\Omega \) und alle regulären, stückweise stetig differenzierbaren Kurvenparametrisierungen \( \gamma \) und \( \widetilde\gamma \) mit gleichem Anfangspunkt \( x \) und gleichem Endpunkt \( y \) und Bild in \( \Omega \) gilt \[ \int\limits_\gamma\langle f(x),dx\rangle=\int\limits_{\widetilde\gamma}\langle f(x),dx\rangle\,. \]
Bemerkung: Stetige Vektorfelder auf Gebieten sind demnach also genau dann wegunabhängig, wenn gilt \[ \int\limits_\gamma\langle f(x),dx\rangle=0 \] für jede reguläre, stückweise stetig differenzierbare und einfach geschlossene Kurve in \( \Omega \) mit Parametrisierung \( \gamma(t). \) Nach obigem Satz sind solche Felder sogar wegunabhängig, wenn sie ein Potential besitzen.
Es gilt aber nun der folgende
Satz: Es seien \( \Omega\subseteq\mathbb R^n \) ein Gebiet und \( f\in C^0(\Omega,\mathbb R^n) \) eine Abbildung. Dann ist \( f(x) \) genau dann wegunabhängig in \( \Omega, \) wenn \( f(x) \) ein Gradientenfeld ist und ein Potential \( \varphi(x)\in C^1(\Omega,\mathbb R) \) besitzt.
Beweis
Aus der Wegunabhängigkeit und der Stetigkeit von \( f(x) \) müssen wir nur noch auf die Existenz eines Potentials schließen, denn die andere Richtung haben wir eben gezeigt. Dazu gehen wir in mehreren Schritten vor.
| 1. | Wähle ein \( x^*\in\Omega. \) Es bezeichne \( \gamma_x\colon[0,1]\to\Omega \) eine die Punkte \( x^* \) und \( x\in\Omega \) verbindende, ganz in \( \Omega \) liegende, stückweise stetig differenzierbare Kurve mit \( \gamma_x(0)=x^* \) und \( \gamma_x(1)=x. \) Wir setzen |
\[ \varphi(x):=\int\limits_{\gamma_x}\langle f(\xi),d\xi\rangle\,,\quad x\in\Omega. \]
| Das Integral ist nach Voraussetzung wegunabhängig. Wir zeigen, dass \( \varphi(x) \) vollständig differenzierbar ist im Sinne unserer ➝ Definition aus der Analysis 2, Kapitel 13, Paragraph 13.2.2. | |
| 2. | Da \( \Omega\subseteq\mathbb R^n \) offen ist, existiert zu beliebigem \( x\in\Omega \) ein \( \varepsilon\gt 0 \) mit |
\[ B_\varepsilon(x):=\{y\in\Omega\,:\,\|x-y\|_2\lt\varepsilon\}\subset\Omega. \]
| Für jeden Vektor \( \delta\in\mathbb R^n \) mit \( \|\delta\|_2\lt\varepsilon \) liegt dann auch die die beiden Punkte \( x\in B_\varepsilon(x) \) und \( x+\delta\in B_\varepsilon(x) \) verbindende gerade Strecke |
\[ \sigma_x(t):=x+t\delta,\quad t\in[0,1], \]
| vollständig in \( B_\varepsilon(x). \) | |
| 3. | Sei nun mit obigen Bezeichnungen \( \gamma_{x+\delta}(t) \) eine stetige, stückweise stetig differenzierbare und vollständig in \( \Omega \) gelegene Kurve. Aus der Wegunabhängigkeit von \( f(x) \) (zweite Zeile in nachstehender Rechnung) schließen wir |
\[ \begin{array}{lll} \varphi(x+\delta)-\varphi(x)\negthickspace & = & \negthickspace\displaystyle \int\limits_{\gamma_{x+\delta}}\langle f(\xi),d\xi\rangle-\int\limits_{\gamma_x}\langle f(\xi),d\xi\rangle \\ & = & \negthickspace\displaystyle \int\limits_{\gamma_x+\sigma_x}\langle f(\xi),d\xi\rangle-\int\limits_{\gamma_x}\langle f(\xi),d\xi\rangle \\ & = & \negthickspace\displaystyle \int\limits_{\gamma_x}\langle f(\xi),d\xi\rangle+\int\limits_{\sigma_x}\langle f(\xi),d\xi\rangle-\int\limits_{\gamma_x}\langle f(\xi),d\xi\rangle \\ & = & \negthickspace\displaystyle \int\limits_{\sigma_x}\langle f(\xi),d\xi\rangle \,=\,\int\limits_0^1\langle f(\sigma_x(t)),\sigma_x'(t)\rangle\,dt \\ & = & \negthickspace\displaystyle \int\limits_0^1\langle f(x+t\delta),\delta\rangle\,dt \end{array} \]
| und damit |
\[ \varphi(x+\delta)-\varphi(x)-\langle f(x),\delta\rangle=\int\limits_0^1\langle f(x+t\delta)-f(x),\delta\rangle\,dt. \]
| 4. | Hiermit schätzen wir nun wie folgt ab |
\[ \begin{array}{lll} |\varphi(x+\delta)-\varphi(x)-\langle f(x),\delta\rangle|\negthickspace & \le & \negthickspace\displaystyle \int\limits_0^1|f(x+\delta)-f(x)||\delta|\,dt \\ & \le & \negthickspace\displaystyle |\delta|\cdot\int\limits_0^1|f(x+\delta)-f(x)|\,dt, \end{array} \]
| worin wir wegen der Stetigkeit und sogar lokalen gleichmäßigen Stetigkeit beachten |
\[ \int\limits_0^1|f(x+\delta)-f(x)|\,dt\longrightarrow 0\quad\mbox{für}\ |\delta|\to 0. \]
| Also ist \( \varphi(x) \) vollständig differenzierbar, d.h. es gilt für \( |\delta|\gt 0 \) hinreichend klein |
\[ \varphi(x+\delta)=\varphi(x)+\langle f(x),\delta\rangle+o(|\delta|), \]
| und der erste Satz aus Paragraph 13.2.2 besagt |
\[ \nabla\varphi(x)=f(x)\quad\mbox{in}\ \Omega. \]
Also ist \( f(x) \) ein Gradientenfeld mit Potential \( \varphi\in C^1(\Omega,\mathbb R).\qquad\Box \)
Definition: Es sei \( \Omega\subseteq\mathbb R^n \) eine offene Menge. Eine reelle Pfaffsche Form oder Differentialform erster Ordnung oder kurz \( 1 \)-Form ist eine Abbildung \[ \omega\colon\Omega\longrightarrow L(\mathbb R^n,\mathbb R) \] von \( \Omega \) in die Menge \( L(\mathbb R^n,\mathbb R) \) der reellwertigen, stetigen Linearformen.
Jedem Punkt \( x\in\Omega \) wird also eine solche Linearform zugeordnet. Ist genauer \( x\in\Omega \) ein Punkt, so stellt (wir schreiben zur Deutlichkeit \( \omega_x \) statt \( \omega(x) \)) \[ \omega_x\colon\mathbb R^n\longrightarrow\mathbb R \] eine reellwertige lineare Abbildung dar.
Beispiel: Eine vollständig differenzierbare Abbildung \( f\colon\Omega\to\mathbb R \) erfüllt \[ f(x+h)=f(x)+\langle\nabla f(x),h\rangle+o(h),\quad x\in\Omega, \] mit dem Gradienten \( \nabla f(x)\in\mathbb R^n. \) Die \( 1 \)-Form, um die es hier geht, lautet \[ \omega_x\colon\mathbb R^n\longrightarrow\mathbb R \quad\mbox{vermöge}\quad \omega_x(h)=\langle\nabla f(x),h\rangle\,,\quad x\in\Omega. \]
Wir wollen nun Normalformen für Pfaffsche Formen ableiten.
| 1. | Zunächst bezeichnen wir mit |
\[ x_i\colon\mathbb R^n\longrightarrow\mathbb R \quad\mbox{vermöge}\quad x_i(\xi):=\xi_i\ \mbox{für}\ \xi=(\xi_1,\ldots,\xi_n)\in\mathbb R^n \]
| die \( i \)-te Koordinatenabbildung. Diese genügt |
\[ x_i(\xi+h)=\xi_i+h_i\,,\quad i=1,\ldots,n, \]
| und wir erhalten für ihr Differential erster Ordnung in \( \xi\in\mathbb R^n, \) angewandt auf \( h\in\mathbb R^n, \) |
\[ \langle\nabla x_i(\xi),h\rangle=h_i\,, \]
| siehe das vorige Beispiel. Für dieses Differential schreiben wir \( dx_{i,\xi}(h). \) | |
| 2. | Es bezeichnen nun die Vektoren \( e_i\in\mathbb R^n, \) \( i=1,\ldots,n, \) die Standardbasisvektoren des \( \mathbb R^n, \) und es sei \( \omega \) eine \( 1 \)-Form. Wir setzen |
\[ a_i(\xi):=\omega_\xi(e_i),\quad i=1,\ldots,n. \]
| Unter Beachtung der Linearität der Differentialform ermitteln wir für den obigen Vektor \( h=h_1e_1+\ldots+h_ne_n \) |
\[ \begin{array}{lll} \omega_\xi(h)\negthickspace & = & \negthickspace\displaystyle \omega_\xi(h_1e_1+\ldots+h_ne_n) \,=\,\sum_{i=1}^n\omega_\xi(h_ie_i) \\ & = & \negthickspace\displaystyle \sum_{i=1}^n\omega_\xi(e_i)h_i \,=\,\sum_{i=1}^na_i(\xi)h_i \,=\,\sum_{i=1}^na_i(\xi)dx_{i,\xi}(h). \end{array} \] Für diese letzte Identität schreiben wir kurz \[ \omega=a_1\,dx_1+\ldots+a_n\,dx_n\,. \] Das ist die gesuchte Normalform einer Differentialform erster Ordnung.
Beispiel: Es sei \( \omega \) das Differential erster Ordnung einer Funktion \( f\in C^1(\Omega,\mathbb R), \) \[ a_i(\xi) =\omega_\xi(e_i) =\langle\nabla f(\xi),e_i\rangle =\frac{\partial f(\xi)}{\partial x_i}\,. \] Dann erhalten wir die Darstellung in Normalform \[ \omega=df=\frac{\partial f}{\partial x_1}\,dx_1+\ldots+\frac{\partial f}{\partial x_n}\,dx_n\,. \]
Beispiel: Jedem Vektorfeld \( \nu\colon\Omega\to\mathbb R^n \) können wir vermittels \[ \omega_{x,\nu}(h):=\langle\nu(x),h\rangle\,,\quad x\in\Omega, \] eine \( 1 \)-Form \( \omega_{x,\nu} \) zuordnen. Ist umgekehrt \( \omega \) eine \( 1 \)-Form auf \( \Omega, \) so existiert zu jeder Linearform \( \omega_x, \) \( x\in\Omega, \) ein eindeutig bestimmter Vektor \( \nu_\omega(x)\in\mathbb R^n \) mit \[ \omega_x(h)=\langle\nu_\omega(x),h\rangle\,. \] Diese gegenseitige Korrespondenz bezeichnet man als den Rieszschen Darstellungssatz. Sind also die \( 1 \)-Form \( \omega \) und das Vektorfeld \( \nu\in\mathbb R^n \) auf diese Weise gegenseitig zugeordnet, so haben wir \[ a_i(\xi)=\langle\nu(\xi),e_i\rangle=\nu_i(\xi) \] bzw. in Normalform \[ \omega=\nu_1\,dx_1+\ldots+\nu_n\,dx_n\,. \]
Wir stellen uns nun die Frage, wie \( 1 \)-Formen entlang regulärer Kurven integriert werden können. Sei dazu eine \( 1 \)-Form \[ \omega=\sum_{i=1}^na_i\,dx_i \] mit stetigen Koeffizienten \( a_i\in C^0(\Omega,\mathbb R) \) vorgelegt. Sei ferner \( \gamma\colon[a,b]\to\Omega \) eine reguläre Kurvenparametrisierung. In Anschluss an unsere bisherigen Betrachtungen definieren wir dann das Kurvenintegral von \( \omega \) entlang \( \gamma(t) \) gemäszlig; \[ \int\limits_\gamma\omega :=\int\limits_a^b\omega_{\gamma(t)}(\dot\gamma(t))\,dt =\int\limits_a^b\sum_{i=1}^na_i(\gamma(t))\dot\gamma(t)\,dt. \] Auch diese Setzung kann unmittelbar auf stückweise stetig differenzierbare Kurven ausgedehnt werden.
19.3.7 Aufgaben und Wiederholungsfragen
| 1. | Was verstehen wir unter einer regulären, stückweise stetig differenzierbaren Kurvenparametrisierung. |
| 2. | Was verstehen wir unter einer regulären, stückweise stetig differenzierbaren Kurve? |
| 3. | Was versteht man unter einem Kurvenintegral? |
| 4. | Berechnen Sie das Kurvenintegral |
\[ \int\limits_C\langle f(x,y),d(x,y)\rangle \]
| worin \( C\subset\mathbb R^2 \) der Einheitskreis als Bild der regulären Parametrisierung |
\[ C\,:\,\gamma(t)=(\cos t,\sin t),\quad t\in[0,2\pi), \]
| bedeutet und |
\[ f\in C^0(\mathbb R^2,\mathbb R^2) \quad\mbox{vermöge}\quad f(x,y)=(-y,x),\ (x,y)\in\mathbb R^2\,. \]
| 5. | Berechnen Sie das Kurvenintegral |
\[ \int\limits_C\langle f(x,y),d(x,y)\rangle \]
| worin \( C\subset\mathbb R^3 \) eine Spiralkurve als das Bild der regulären Parametrisierung |
\[ C\,:\,\gamma(t)=(\cos t,\sin t,t),\quad t\in[0,2\pi), \]
| bedeutet und |
\[ f\in C^0(\mathbb R^3,\mathbb R^3) \quad\mbox{vermöge}\quad f(x,y,z)=(-y,x,z^3),\ (x,y,z)\in\mathbb R^2\,. \]
| 6. | Es seien \( f\colon\mathbb R^n\to\mathbb R^n \) eine stetige Abbildung und \( C\subset\mathbb R^n \) eine reguläre Kurve mit regulärer Kurvenparametrisierung \( \gamma\in C^1([a,b],\mathbb R^n). \) Zeigen Sie |
\[ \left|\,\int\limits_\gamma\langle f(x),dx\rangle\right| \le\max_{t\in[a,b]}\|f(\gamma(t))\|_2\cdot{\mathcal L}[C] \]
| mit der Euklidischen Norm \( \|\cdot\|_2 \) und dem Längenfunktional |
\[ {\mathcal L}[C]:=\int\limits_a^b\sqrt{\dot\gamma_1(t)^2+\ldots+\dot\gamma_n(t)^2}\,dt. \]
| 7. | Wir definiert man die Summe und das Inverse regulärer, stückweise stetig differenzierbarer Kurvenparametrisierungen? |
| 8. | Wie integriert man über Summe und Inverses regulärer, stückweise stetig differenzierbarer Kurvenparametrisierungen? |
| 9. | Formulieren und beweisen Sie den Satz aus Paragraph 19.3.4. |
| 10. | Wann heißt eine Abbildung \( f\in C^0(\Omega,\mathbb R^n) \) wegunabhängig in \( \Omega? \) |
| 11. | Wir betrachten zwei die Punkte \( x_0=(0,0) \) und \( x_1=(1,1) \) verbindende, stetig differenzierbare Kurven \( C_1 \) und \( C_2 \) mit folgenden regulären Parametrisierungen: |
\[ \begin{array}{lll} C_1\ :\ \gamma_1(t)=(t,t), \\ C_2\ :\ \gamma_2(t)=(t,t^2), \end{array} \]
| jeweils für \( t\in[0,1]. \) Zu bestimmen sind die Kurvenintegrale entlang \( C_1\subset\mathbb R^2 \) und \( C_2\subset\mathbb R^2 \) der folgenden Abbildungen | |||||
|
|||||
| Erklären Sie jeweils. | |||||
| 12. | Wir betrachten die Abbildung |
\[ f(x,y)=\left(-\frac{y}{x^2+y^2}\,,\frac{x}{x^2+y^2}\right),\quad(x,y)\in\mathbb R^2\setminus\{(0,0)\}\,. \]
|
\[ \mbox{div}\,f(x,y)=0\quad\mbox{für alle}\ (x,y)\in\mathbb R^2\setminus\{(0,0)\}\,. \]
|
\[ \frac{\partial f_1(x,y)}{\partial x_2}=\frac{\partial f_2(x,y)}{\partial x_1}\quad\mbox{in}\ \mathbb R^2\setminus\{(0,0)\}\,. \]
|
\[ \int\limits_{\partial B}\langle f(x,y),d(x,y)\rangle \]
|
\[ B:=\{(x,y)\in\mathbb R^2\,:\,x^2+y^2\lt 1\}\,. \]
|
\[ \Omega:=\mathbb R^2\setminus\{(x,y)\in\mathbb R^2\,:\,x\le 0,\ y=0\}\,. \]
|
Rechenaufgaben: 4, 5, 6, 9, 11, 12
19.4.1 Flächen und ihre Parametrisierungen
Wir wollen nun Integrale über Flächen \( M\subset\mathbb R^n \) in Euklidischen Räumen studieren.
Wir betrachten zwei stetig partiell differenzierbare Flächenparametrisierungen \[ X\colon\Sigma\longrightarrow\mathbb R^3 \quad\mbox{und}\quad \widetilde X\colon\widetilde\Sigma\longrightarrow\mathbb R^3 \] auf beschränkten, „glatt“ berandeten (später genauer, jetzt z.B. berandet durch eine einfach geschlossene, stetig differenzierbare Kurve) Gebieten \( \Sigma,\widetilde\Sigma\subset\mathbb R^2. \) Beachten Sie die Dimensionszahl \( n=3. \)
Reguläre Flächen
Für solche Flächenparametrisierungen sei Folgendes richtig:
| \( \circ \) | Es existiert eine reguläre Parametertransformation, d.h. eine \( C^1 \)-reguläre, diffeomorphe Abbildung |
\[ \Phi\colon\widetilde\Sigma\longrightarrow\Sigma \]
| mit einer Inversen \( \Phi^{-1}\in C^1(\Sigma,\widetilde\Sigma), \) so dass für die Determinante der Funktionalmatrix \( J_\Phi(\widetilde u,\widetilde v) \) gilt |
\[ \mbox{det}\,J_\Phi(\widetilde u,\widetilde v) =\mbox{det}\left(\frac{\partial(\varphi_1(\widetilde u,\widetilde v),\varphi_2(\widetilde u,\widetilde v))}{\partial(u,v)}\right)\not=0 \quad\mbox{für alle}\ (\widetilde u,\widetilde v)\in\widetilde\Sigma \]
| mit \( \Phi=(\varphi_1,\varphi_2) \) (je nach Vorzeichen orientierungstreu oder orientierungsumkehrend) mit |
\[ \widetilde X(\widetilde u,\widetilde v)=X\circ\Phi(\widetilde u,\widetilde v)=X(\Phi(\widetilde u,\widetilde v)),\quad(\widetilde u,\widetilde v)\in\widetilde\Sigma\,. \]
| \( \circ \) | \( X\in C^1(\Sigma,\mathbb R^3) \) genüge der geometrischen Regularitätsbedingung |
\[ \mbox{Rang}\,\partial X(u,v) =\mbox{Rang} \left( \begin{array}{cc} x_{1,u}(u,v) & x_{1,v}(u,v) \\ x_{2,u}(u,v) & x_{2,v}(u,v) \\ x_{3,u}(u,v) & x_{3,v}(u,v) \end{array} \right) =2 \quad\mbox{für alle}\ (u,v)\in\Sigma \] mit \( X=(x_1,x_2,x_3). \) Eine solche Parametrisierung \( X\in C^1(\Sigma,\mathbb R^3), \) die also analytisch wie geometrisch regulär ist, bezeichnen wir kurz als regulär. Es heißen \( X(u,v) \) und \( \widetilde X(\widetilde u,\widetilde v) \) äquivalent, in Zeichen \( X\sim\widetilde X. \)
Die Äquivalenzklasse \( [X] \) aller zu \( X(u,v) \) äquivalenten Flächenparametrisierungen bezeichnet man häufig als reguläre Fläche. Wie auch bei Kurven, können wir uns stillschweigend dieser Definition anschließen, aber auch jetzt steht für uns vor allem das geometrische Bild \[ M=\mbox{Spur}\,X(u,v)\subset\mathbb R^n \] im Vordergrund, welches wir auch als reguläre Fläche bezeichnen möchten. Eine genaue Definition wollen wir aber auslassen.
Bemerkung: Es wird wichtig, Differenzierbarkeit der Parametrisierungen bis zum Rand \( \partial\Sigma \) des Parametergebiets \( \Sigma \) zu fordern. Zu diesem Zweck wollen wir ebenfalls stillschweigend voraussetzen, dass \[ X\in C^1(\Omega,\mathbb R^3) \quad\mbox{bzw.}\quad X\in C^k(\Omega,\mathbb R^3)\ \mbox{für ein}\ k\ge 1 \] richtig ist mit einer offenen Menge \( \Omega\subset\mathbb R^2 \) mit der Eigenschaft \( \Sigma\subset\subset\Omega. \)
19.4.2 Tangentialraum und Normalenraum
Wir bezeichnen die reguläre Abbildung bzw. ihr Bild \( M\subset\mathbb R^3 \) auch als
| \( \circ \) | Immersion, falls \( X\in C^1(\Sigma,\mathbb R^3) \) der geometrischen Regularitätsbedingung genügt |
\[ \mbox{Rang}\,\partial X(u,v)=2\quad\mbox{für alle}\ (u,v)\in\Sigma, \]
| \( \circ \) | Einbettung, falls \( X\colon\Sigma\to\mathbb R^3 \) zusätzlich injektiv ist. |
Die geometrische Regularität sichert, dass die von den beiden Tangentialvektoren \[ \begin{array}{lll} X_u(u,v)\negthickspace & = & \negthickspace\displaystyle (x_{1,u}(u,v),x_{2,u}(u,v),x_{3,u}(u,v)), \\ X_v(u,v)\negthickspace & = & \negthickspace\displaystyle (x_{1,v}(u,v),x_{2,v}(u,v),x_{3,v}(u,v)) \end{array} \] aufgespannte Tangentialebene \( T_X(u,v) \) im Punkt \( (u,v)\in\Sigma \) stets zweidimensional ist: \[ \mbox{dim}\,T_X(u,v)=\mbox{dim}\,\mbox{Lin}\,\{X_u(u,v),X_v(u,v)\}=2\quad\mbox{für alle}\ (u,v)\in\Sigma\,. \] Wir definieren hierzu noch den Einheitsnormalenvektor \[ N(u,v):=\frac{X_u(u,v)\times X_v(u,v)}{|X_u(u,v)\times X_v(u,v)|}\,,\quad(u,v)\in\Sigma, \] wobei auf Grund der geometrischen Regularitätsbedingung und damit der linearen Unabhängigkeit der Tangentialvektoren zu beachten ist \[ |X_u(u,v)\times X_v(u,v)|\gt 0\quad\mbox{für alle}\ (u,v)\in\Sigma. \] Statt „Tangentialebene“ benutzt man auch den allgemeineren Begriff des Tangentialraums, und als Normalenraum verstehen wir die lineare Hülle des Einheitsnormalenvektors \( N(u,v). \)
19.4.3 Erste Fundamentalform und Flächeninhalt
Von grundlegender Bedeutung ist der Begriff der ersten Fundamentalform \[ I(X):=(g_{ij})_{i,j=1,2}\subset\mathbb R^{2\times 2} \quad\mbox{mit}\quad g_{ij}(u,v):=\langle X_{u^i}(u,v),X_{u^j}(u,v)\rangle \] und den Setzungen \( u^1:=u \) und \( u^2:=v. \) Immersionen erfüllen stets \[ \mbox{det}\,I(X)=g_{11}g_{22}-g_{12}^2\gt 0\quad\mbox{in}\ \Sigma, \] was also eine weitere Form der geometrischen Regularitätsbedingung bedeutet, denn es gilt \[ |X_u(u,v)\times X_v(u,v)|=\sqrt{\mbox{det}\,I(X)}\,. \] Man bezeichnet \[ W(u,v):=|X_u(u,v)\times X_v(u,v)|,\quad(u,v)\in\Sigma, \] als Oberflächenelement. Als Flächeninhalt einer Immersion \( X\in C^1(\Sigma,\mathbb R^3) \) definieren wir \[ {\mathcal A}[X]:=\int\limits_\Sigma W(u,v)\,d\ell_2(u,v). \]
Satz: Der Wert des Flächeninhalts \( {\mathcal A}[X] \) der Immersion \( X\in C^1(\Sigma,\mathbb R^3) \) ist invariant gegenüber regulären Umparametrisierungen.
Wir wollen die geometrische Bedeutung der ersten Fundamentalform anhand des folgenden Beispiels verdeutlichen.
Beispiel: Für die Länge einer stetig differenzierbaren Flächenkurve auf dem Bild \( M\subset\mathbb R^3 \) der Immersion \( X\in C^1(\Sigma,\mathbb R^3), \) also \[ c\colon[a,b]\longrightarrow M \quad\mbox{vermöge}\quad c(t):=X\circ\gamma(t),\ t\in[a,b], \] mit \( \gamma\in C^1([a,b],\Sigma) \) und \( \gamma(t)=(u(t),v(t)) \) ermitteln wir (als Übung) \[ {\mathcal L}[c] =\int\limits_a^b|c'(t)|\,dt =\int\limits_a^b\sqrt{g_{11}\dot c_1(t)^2+2g_{12}\dot c_1(t)\dot c_2(t)+g_{22}\dot c_2(t)^2}\,dt. \]
19.4.4 Approximation von Länge und Flächeninhalt
Mehrmals haben wir bereits vom Längenfunktional \[ {\mathcal L}[C]=\int\limits_a^b|c'(t)|\,dt,\quad C:=\mbox{Spur}\,c([a,b])\ (\mbox{oder einfach}\ c([a,b])), \] sowie vom Flächeninhaltsfunktional \[ {\mathcal A}[M]=\int\limits_\Sigma|X_u(u,v)\times X_v(u,v)|\,dudv,\quad M:=X(\Sigma), \] Gebrauch gemacht. Wir wollen nun anschaulich und mit nur wenigen Details eine mengentheoretische und eine geometrische Approximation dieser Funktionale kennenlernen.
Das eindimensionale normierte Hausdorffmaß
In ➝ Abschnitt 18.1 haben wir das Hausdorffsche Überdeckungsmaß \( {\mathcal H}^s(\Omega) \) für eine beliebige Menge \( \Omega\subseteq\mathbb R^n \) kennengelernt, siehe auch das nachstehende Bild. Im Falle \( \Omega=\mbox{Spur}\,c([a,b]) \) mit einer eineindeutigen (beachte, dass es sich um ein Überdeckungsmaß handelt), Lipschitzstetigen Kurvenparametrisierung \( c\colon[a,b]\to\mathbb R^n \) gilt \[ {\mathcal H}_*^1(\Omega)=\int\limits_{[a,b]}|c'(t)|\,d\ell_1(t), \] d.h. \( {\mathcal H}_*^1(\Omega) \) gibt die (differentialgeometrische) Länge der Kurve wieder, siehe Evans, L.C. und Gariepy, R.F.: Measure theory and fine properties of functions, Abschnitt 3.3, Paragraph 3.3.4, erstes Beispiel. Hierbei bezeichnen wir mit \[ {\mathcal H}_*^s(\Omega) :=\inf \left\{ \sum_{k\ge 1}\alpha(s)\left(\frac{\mbox{diam}\,\Omega_i}{2}\right)^s\,:\, \{\Omega_i\}_{i=1,2,\ldots}\ \mbox{ist \( \delta \)-Überdeckung von}\ \Omega \right\} \] das (im Gegensatz zu \( {\mathcal H}^s(\Omega) \) aus Kapitel 18) normierte Hausdorffmaß, worin \[ \alpha(s):=\frac{\pi^\frac{s}{2}}{\Gamma\left(\frac{s}{2}+1\right)} \] ein dimensionsabhängiger Faktor bedeutet mit der Gamma-Funktion \[ \Gamma(u):=\int\limits_0^\infty e^{-x}x^{u-1}\,dx,\quad 0\lt u\lt\infty\,. \] Beachte insbesondere \( \alpha(0)=0 \) und \( \alpha(1)=2, \) so dass tatsächlich gilt \( {\mathcal H}^1(\Omega)={\mathcal H}_*^1(\Omega) \) mit dem aus vorigem Kapitel 18 bekannten (nichtnormierten) Hausdorffmaß \( {\mathcal H}^1(\Omega). \) Zur korrekten Formulierung der folgenden geometrischen und mengentheoretischen Resultate ist es jedoch zweckmäßig, das normierte Hausdorffmaß \( {\mathcal H}_*^s(\Omega) \) zu verwenden.
Die Jordanlänge
Es sei \( c\colon[a,b]\to\mathbb R^n \) stetig auf dem kompakten Intervall \( [a,b]\subset\mathbb R. \) Wir betrachten ein Zerlegung von \( [a,b] \) gemäß \[ a=t_0\lt t_1\lt t_2\lt\ldots\lt t_N=b,\quad N\in\mathbb N, \] siehe auch nachstehendes Bild. Dann gibt \[ \sum_{k=1}^N|c(t_k)-c(t_{k-1})| \] die Länge des durch die Kurvenpunkte \( c(t_0),\ldots,c(t_N) \) verlaufenden Polygons.
Unter der Jordanlänge der Kurve \( C=\mbox{Spur}\,c([a,b]) \) verstehen wir nun den Ausdruck \[ {\mathcal L}[C]:=\sup\sum_{i=1}^N|c(t_k)-c(t_{k-1})|, \] wobei das Supremum über alle möglichen endlichen Zerlegungen von \( [a,b] \) gebildet wird. Die Kurve \( C \) heißt ferner rektifizierbar, wenn \( {\mathcal L}[C]\lt\infty \) richtig ist.
Diese Definition geht zurück auf
| \( \circ \) | Jordan, C.: Cours d'Analyse de l'Ecole Polytechnique. 1884. |
| \( \circ \) | Scheeffer, L.: Allgemeine Untersuchungen über Rectification der Curven. 1884. |
Gibt es einen Zusammenhang zum eindimensionalen normierten Hausdorffmaß \( {\mathcal H}_*^1(C)? \)
Zunächst ist die Kurve \( C=\mbox{Spur}\,c([a,b]) \) genau dann rektifizierbar, wenn die Komponenten \( c_i(t) \) auf \( [a,b]\subset\mathbb R \) von beschränkter Variation sind, wobei wir zur Definition dieser, der Rektifizierbarkeit sehr nahe liegenden Regularitätsklasse auf folgenden ➝ Wikipedia-Artikel verweisen.
Nun argumentieren wir wie folgt:
| \( \circ \) | Sind die Komponenten \( c_i(t) \) Lipschitzstetig auf \( [a,b]\subset\mathbb R, \) so sind sie auch von beschränkter Variation. Insbesondere ist auch der Vektor \( c(t) \) Lipschitzstetig auf \( [a,b]. \) |
| \( \circ \) | Ist die Kurve \( C \) rektifizierbar, so gilt |
\[ {\mathcal H}_*^1(C)={\mathcal L}[C], \]
| siehe insbesondere Lemma 5.4 aus der Monographie Falconer, K.: Fractal geometry, 2014. | |
| \( \circ \) | Nach den vorigen Ausführungen zum eindimensionalen normierten Hausdorffmaß gilt daher |
\[ {\mathcal L}[C]=\int\limits_{[a,b]}|c'(t)|\,d\ell_1(t). \]

Das zweidimensionale normierte Hausdorffmaß
Das zweidimensionale normierte Hausdorffmaß als Überdeckungsmaß gibt den Flächeninhalt einer hinreichend regulären Fläche im \( \mathbb R^3 \) wieder, genauer nämlich
| \( \circ \) | eines Flächengraphen |
\[ X(u,v)=(u,v,f(u,v)),\quad(u,v)\in\Sigma, \]
| mit einer Lipschitzstetigen, den Graphen erzeugenden Funktion \( f(u,v), \) so dass gilt |
\[ {\mathcal H}_*^2(M)=\int\limits_\Sigma\sqrt{1+|\nabla f(u,v)|^2}\,d\ell_2(u,v) \]
| mit \( M=\{(u,v,f(u,v))\,:\,(u,v)\in\Sigma\}\subset\mathbb R^3, \) | |
| \( \circ \) | oder des Bildes einer parametrischen, eineindeutigen und Lipschitzstetigen Abbildung |
\[ X(u,v)=(x(u,v),y(u,v),z(u,v)),\quad(u,v)\in\Sigma, \]
| und in diesem Fall gilt |
\[ {\mathcal H}_*^2(M)=\int\limits_\Sigma\sqrt{g_{11}g_{22}-g_{12}^2}\,d\ell_2(u,v) \]
| mit \( M=X(\Sigma) \) und den Koeffizienten \( g_{ij} \) der ersten Fundamentalform von \( X(u,v), \) siehe erneut Evans, L.C. und Gariepy, R.F.: Measure theory and fine properties of functions, Abschnitt 3.3, Paragraph 3.3.4, zweites, drittes und viertes Beispiel. |

Das Beispiel von Peano und Schwarz
Das folgende Beispiel geht auf G. Peano (in einer Vorlesung im Mai 1882) und H.A. Schwarz (in einem Brief vom 25. Dezember 1880 an A. Genocchi) zurück - siehe Cesari, L.: Surface area. Princeton University Press 1956, Seite 25.
Wir betrachten einen Kreiszylinder vom Radius \( r\gt 0 \) und mit der Höhe \( h\gt 0, \) parametrisiert durch \[ X(u,v)=(r\cos u,r\sin u,v),\quad u\in[0,2\pi],\ v\in[0,h]. \] Die Nichteineindeutigkeit der Parametrisierung an den Rändern \( u=0 \) und \( u=2\pi \) ist für das Folgende unerheblich.
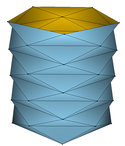
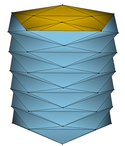
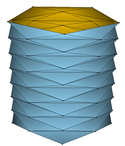
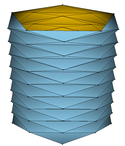
Wir zerlegen nun den \( u \)-Bereiches \( [0,2\pi] \) in \( m\ge 4 \) äquidistante Teile und den \( v \)-Bereiches in \( n\ge 1 \) äquidistante Teile. Es ergeben sich \( m\cdot n \) abgeschlossene, bis auf ihre Ränder zueinander disjunkte Rechtecke, die in ihrer Vereinigung den gesamten Parameterbereich ergeben. Schließlich zerlegen wir, wie im nachstehenden Bild veranschaulicht, sämtliche Teilrechtecke in gleichschenklige Dreiecke, beginnend mit \( m \) aufrecht stehenden Dreiecken entlang \( v=0 \) der gemeinsamen Höhen \( \frac{h}{n}. \)
Unser Bild zeigt den Fall \( m=4 \) und \( n=6: \)
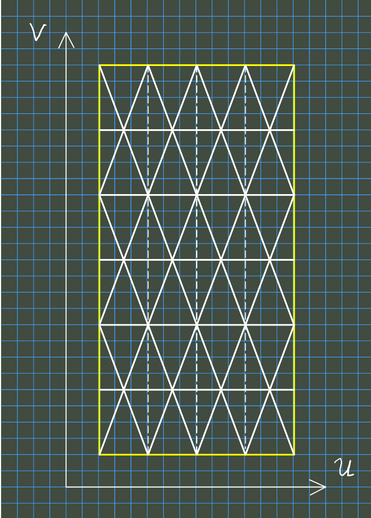
Im Bild denken wir uns nun die Ecken der beschriebenen Dreiecke, die den Parameterbereich aufspannen, auf der Zylinderwand anliegen, d.h. nur diese Eckpunkte werden vermittels \( X(u,v) \) in den Raum abgebildet. Diese Bildpunkte sind gleichzeitig die Eckpunkte einer aus gleichschenkligen Dreiecken aufgebauten Polyederfläche im Raum, die den Zylinder von innen „approximiert“.
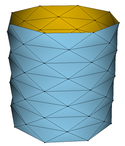
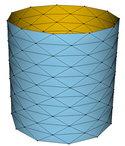
Unter Verwendung der Software Javaview veranschaulichen wir diese Situation:
| \( \circ \) | die obere Zeile zeigt die Fälle \( (m,n)\in\{(5,5),(8,8),(11,11),(14,14),(17,17)\}; \) |
| \( \circ \) | die mittlere Zeile zeigt die Fälle \( m\in\{8,11,14,17\} \) und \( n=5; \) |
| \( \circ \) | die untere Zeile zeigt die Fälle \( m=5 \) und \( n\in\{8,11,14,17\}. \) |
Die untere Zeile macht das Problem deutlich: Die Flächen der einzelnen Bilddreiecke aufsummiert, ergibt einen Gesamtinhalt, der den elementaren Inhalt \( 2\pi rh \) des Zylinders übertreffen wird - was wir als Übung belassen.







Der Lebesgue-Geöcze-Inhalt
Man betrachtet nun alle möglichen polyedrischen Approximationen des Zylindermantels - oder eben irgendeiner zu untersuchenden stetigen Fläche, ermittelt die elementargeometrischen Inhalte der Approximationen und bildet hiervon das Infimum. Genauer
| \( \circ \) | stellte H. Lebesgue 1902 die Voraussetzung, dass die Polyederapproximationen gleichmäßig gegen Fläche konvergieren, |
| \( \circ \) | und 1910 stellte Z. de Geöcze die Vermutung auf, dass es hierbei genügt, nur Polyederapproximationen zu betrachten, deren Ecken auf der Fläche liegen, eben wie in unserem Zylinderbeispiel. |
Wir verweisen dabei auf die dreiteilige Arbeit von Toralballa, L.V.: A geometric theory of surface area (1969, 1972, 1973).
Der Lebesgue-Geöcze-Inhalt stimmt nun mit den uns bekannten analytischen Darstellung für den Inhalt \[ \int\limits_\Sigma\sqrt{1+|\nabla f(x,y)|^2}\,d\ell_2(x,y) \quad\mbox{bzw.}\quad \int\limits_\Sigma\sqrt{g_{11}g_{22}-g_{12}^2}\,d\ell_2(u,v) \] der Fläche \( M\subset\mathbb R^3 \) im Falle eines Flächengraphen \( M=\{(x,y,f(x,y)\,:\,(x,y)\in\Sigma\} \) bzw. im Falle einer parametrischen Einbettung \( X(u,v) \) überein, falls \( f(x,y) \) bzw. \( X(u,v) \) selbst Lipschitzstetig sind (in beiden Fällen ist \( \Sigma\subset\mathbb R^2 \) geeignet vorauszusetzen). So lesen wir in Rademacher, H.: Über partielle und totale Differenzierbarkeit von Funktionen mehrerer Variablen II (1920) auf der zweiten Seite:
Der Inhalt einer über dem Quadrat \( Q \) [bzw. quadrierbares Gebiet] sich hinstreckenden Fläche \( z=f(x,y), \) die der Lipschitzschen Bedingung ... genügt, ist der Limes des Inhaltes einer Folge von Polyedern, die sich gleichfalls schlicht über \( Q \) hinstrecken, und die so beschaffen sind, daß ihre Ecken auf der Fläche liegen, daß die Polyederfolge gegen die Fläche konvergiert und daß die Neigungen der Polyederebenen gegen die Fläche konvergiert und daß die Neigungen der Polyederebenen gegen die Neigungen der Tangentenebenen der Fläche, wo diese existieren, konvergieren. Dabei sollen die Polyeder der Lipschitzschen Bedingung genügen, und zwar gleichmäßig, d.h. mit einer für alle geltenden Konstanten \( M'. \)
19.4.5 Differential-2-Formen und Flächenintegrale
Wir wollen nun Flächenintegrale \[ \int\limits_M(f_1\,dy\wedge dz+f_2\,dz\wedge dx+f_3\,dx\wedge dy) \] einführen.
Definition: Es seien \( M\subset\mathbb R^3 \) eine vermittels der regulären Parametrisierung \[ X(u,v)=(x(u,v),y(u,v),z(u,v)),\quad(u,v)\in\Sigma, \] gegebene Immersion \( X\in C^1(\Sigma,\mathbb R^3) \) und \( f\in C^1(\mathbb R^3,\mathbb R^3) \) eine Abbildung. Dann setzen wir \[ \begin{array}{lll} \displaystyle \int\limits_Mf_1\,dy\wedge dz\negthickspace & := & \negthickspace\displaystyle \int\limits_\Sigma f_1(X(u,v))\,\mbox{det}\,\frac{\partial(y,z)}{\partial(u,v)}\,d\ell_2(u,v), \\ \displaystyle \int\limits_Mf_2\,dz\wedge dx\negthickspace & := & \negthickspace\displaystyle \int\limits_\Sigma f_2(X(u,v))\,\mbox{det}\,\frac{\partial(z,x)}{\partial(u,v)}\,d\ell_2(u,v), \\ \displaystyle \int\limits_Mf_3\,dx\wedge dy\negthickspace & := & \negthickspace\displaystyle \int\limits_\Sigma f_3(X(u,v))\,\mbox{det}\,\frac{\partial(x,y)}{\partial(u,v)}\,d\ell_2(u,v) \end{array} \] und bezeichnen den symbolischen Ausdruck \[ \int\limits_M(f_1\,dy\wedge dz+f_2\,dz\wedge dx+f_3\,dx\wedge dy) \] als (parameterfreies) Flächenintegral.
Bei den Symbolen, den sogenannten Basis-Differential- \( 2 \)-Formen, \[ dy\wedge dz,\quad dz\wedge dx,\quad dx\wedge dy \] ist auf die Reihenfolge der \( 1 \)-Formen zu achten. Beispielsweise ist nach obiger Definition \[ \begin{array}{lll} \displaystyle \int\limits_Mf_1\,dy\wedge dz\negthickspace & = & \negthickspace\displaystyle \int\limits_\Sigma f_1(X(u,v))\,\mbox{det}\,\frac{\partial(y,z)}{\partial(u,v)}\,d\ell_2(u,v) \\ & = & \negthickspace\displaystyle -\,\int\limits_\Sigma f_1(X(u,v))\,\mbox{det}\,\frac{\partial(z,y)}{\partial(u,v)}\,d\ell_2(u,v) \\ & = & \negthickspace\displaystyle -\,\int\limits_Mf_1\,dz\wedge dy, \end{array} \] so dass wir folgerichtig setzen \[ dy\wedge dz=-dz\wedge dy\quad\mbox{usw.} \]
Satz: Es sei \( M\subset\mathbb R^3 \) eine Immersion. Dann ist das Flächenintegral \[ \int\limits_M(f_1\,dy\wedge dz+f_2\,dz\wedge dx+f_3\,dx\wedge dy) \] invariant unter positiv orientierten, regulären Parametertransformationen.
19.4.6 Das Flächenintegral als Flussintegral
Wir wollen Flächenintegrale als Flussintegrale deuten. Dazu betrachten zunächst mit dem Flächenelement \( W(u,v) \) und dem Einheitsnormalenvektor \( N(u,v) \) der Immersion \( X\in C^1(\Sigma,\mathbb R^3) \) \[ WN=X_u\times X_v=(y_uz_v-z_uy_v,z_ux_v-z_vx_u,x_uy_v-y_ux_v) \] bzw. unter Benutzung der obiger Jacobischen Unterdeterminanten \[ WN=\left(\mbox{det}\,\frac{\partial(y,z)}{\partial(u,v)}\,,\mbox{det}\,\frac{\partial(z,x)}{\partial(u,v)}\,,\mbox{det}\,\frac{\partial(x,y)}{\partial(u,v)}\right). \] Damit erhalten wir \[ \begin{array}{l} \displaystyle \int\limits_M(f_1\,dy\wedge dz+f_2\,dz\wedge dx+f_3\,dx\wedge dy) \\ \qquad\displaystyle =\,\int\limits_\Sigma \left\{ f_1(X)\,\mbox{det}\,\frac{\partial(y,z)}{\partial(u,v)} +f_2(X)\,\mbox{det}\frac{\partial(z,x)}{\partial(u,v)} +f_3(X)\,\mbox{det}\,\frac{\partial(x,y)}{\partial(u,v)} \right\}d\ell_2(u,v) \\ \qquad\displaystyle =\,\int\limits_\Sigma\langle(f_1,f_2,f_3),N\rangle\,W\,d\ell_2(u,v). \end{array} \]
| \( \to \) | Es ist also das Flächenintegral |
\[ \int\limits_M(f_1\,dy\wedge dz+f_2\,dz\wedge dx+f_3\,dx\wedge dy) \]
| gleich dem Fluss des Feldes \( f=(f_1,f_2,f_3)\in\mathbb R^3 \) durch die Immersion \( M\subset\mathbb R^3, \) d.h. |
\[ \int\limits_M\langle f,N\rangle\,W\,d\ell_2(u,v). \]
19.4.7 Aufgaben und Wiederholungsfragen
| 1. | Was verstehen wir unter einer regulären Flächenparametrisierung? |
| 2. | Was verstehen wir unter einer regulären Fläche? |
| 3. | Was versteht man unter einer Immersion? |
| 4. | Betrachten Sie die Flächenparametrisierung |
\[ X(u,v)=(v\cos u,v\sin v,\sin v),\quad u\in[0,2\pi),\ v\in[0,4\pi). \]
|
|||||
| 5. | Was versteht man unter einer Einbettung? | ||||
| 6. | Auf \( \Sigma\subset\mathbb R^2, \) wie in Paragraph 19.4.1 beschrieben, sei eine Funktion \( f\in C^1(\Sigma,\mathbb R) \) gegeben, und mit ihr betrachten wir den Flächengraphen |
\[ X(x,y)=(x,y,f(x,y)),\quad(x,y)\in\Sigma. \]
|
|||||
| 7. | Wir betrachten die Parametrisierung |
\[ X(u,v):=(\sin u,\sin u\cos u,v),\quad(u,v)\in(-0.1,\pi+0.1)\times(-1,1). \]
|
|||||
| 8. | Wie sind die Tangentialvektoren einer Immersion \( X(u,v) \) definiert? | ||||
| 9. | Wie ist die Tangentialebene \( T_X(u,v) \) einer Immersion \( X(u,v) \) im Punkt \( (u,v)\in\Sigma \) definiert? | ||||
| 10. | Wir betrachten die Flächenparametrisierung |
\[ X(u,v):=(u,v,u^3-3uv^2),\quad(u,v)\in(-1,1)\times(-1,1). \]
| Berechnen Sie die Tangentialvektoren und die Tangentialebene im Punkt \( (0,0). \) Fertigen Sie eine auch Skizze an. | |
| 11. | Wie ist der Einheitsnormalenvektor \( N(u,v) \) einer Immersion definiert? |
| 12. | Betrachten Sie erneut die Flächenparametrisierung |
\[ X(u,v)=(u,v,u^3-3uv^2),\quad(u,v)\in(-1,1)\times(-1,1), \]
| aus Aufgabe 10. Berechnen Sie den Einheitsnormalenvektor \( N(0,0) \) im Punkt \( (0,0). \) | |
| 13. | Betrachten Sie die Parametrisierung des Möbiusbandes |
\[ X(u,v)=\left(\sin u+v\sin\frac{u}{2}\sin u,\cos u+v\sin\frac{u}{2}\cos u,v\cos\frac{u}{2}\right) \]
| für \( (u,v)\in\mathbb R\times[-1,1] \) - der Parameterbereich ist nicht beschränkt und nicht offen, was uns in dieser Aufgabe aber nicht einschränkt. | |||||
|
\[ X(u,v)=X(u+2\pi,-v)\quad\mbox{für alle}\ (u,v)\in\mathbb R\times[-1,1]. \]
|
\[ X([0,2\pi)\times[-1,1])=X(\mathbb R\times[-1,1]). \]
|
\[ N(u,v)=\frac{X_u(u,v)\times X_v(u,v)}{|X_u(u,v)\times X_v(u,v)|}\,. \]
|
|||
| 14. | Wie ist die Matrix der ersten Fundamentalform \( I(X)=(g_{ij})_{i,j=1,2} \) einer Immersion definiert? | ||
| 15. | Wir betrachten folgende Parametrisierungen der zweidimensionalen Ebene \( z=0, \) nämlich |
\[ \begin{array}{l} X(u,v)=(u,v,0),\quad(u,v)\in\mathbb R^2\,, \\ \widetilde X(r,\varphi)=(r\cos\varphi,r\sin\varphi,0),\quad(r,\varphi)\in[0,\infty)\times[0,2\pi). \end{array} \]
| Berechnen Sie jeweils die Matrix der ersten Fundamentalform und deren Determinante. Sind die Parametrisierungen regulär? |
| 16. | Betrachten Sie folgende Parametrisierung des Kreiszylinders |
\[ X(u,v)=(\cos u,\sin u,v),\quad(u,v)\in[0,2\pi)\times[0,1]. \]
| Berechnen Sie die Matrix der ersten Fundamentalform, und vergleichen Sie mit der ersten Fundamentalform der Abbildung \( X(u,v) \) aus Aufgabe 15. Erläutern Sie. | |
| 17. | Wir betrachten die Abbildung |
\[ X(u,v)=(\sin u\cos v,\sin u\sin v,\cos u),\quad(u,v)\in[0,\pi]\times[0,2\pi). \]
| Ermitteln Sie die Matrix der ersten Fundamentalform. Ist die Parametrisierung regulär? Um welche Fläche handelt es sich? - Auch hier sind unsere Voraussetzungen an den Parameterbereich nicht gänzlich erfüllt, was wir aber in dieser Aufgabe ignorieren. | |
| 18. | Es sei \( X\colon\Sigma\to\mathbb R^3 \) eine Immersion. Verifizieren Sie die Identität |
\[ |X_u(u,v)\times X_v(u,v)|=\sqrt{\mbox{det}\,I(X)}\,. \]
| 19. | Wie ist der Flächeninhalt \( {\mathcal A}(X) \) einer Immersion \( X(u,v) \) definiert? | ||||
| 20. | Studieren Sie das Beispiel aus Paragraph 19.4.3. | ||||
|
Rechenaufgaben: 4, 6, 7, 10, 12, 13, 15, 16, 17, 18, 20